题目内容
1.如图(a),长为L的光滑斜面AB与高台边缘光滑相接,BC为一竖直墙,将小球从斜面AB的顶端静止释放,小球到达斜面底端后恰能无能量损失地从高台边缘水平飞出.高台底部有另一足够长的斜面CD.调节斜面AB的倾角α与斜面CD的倾角β,使小球从斜面AB顶端静止释放后,恰能垂直击中斜面CD.不计空气阻力,重力加速度为g,α、β为锐角.求:
(1)小球在空中飞行时间t(用α、β和L表示)?
(2)某一研究小组取长为L=0.5m的斜面AB进行实验,实验中发现改变斜面AB的倾角α后,为了使从AB顶端静止释放的小球还能垂直击中斜面,只需对应地调整斜面CD的倾角β.多次实验并记录每次α与β的数值,由实验数据得出图(b)所示拟合直线.请问此坐标系的横轴表示什么?试求竖直墙BC的高度h(取g=10m/s2)?
(3)在第(2)问中,该研究小组发现,小球每次垂直打在CD上的落点与竖直墙BC的距离S随α和β的改变而不同.试求小球在CD上的落点离竖直墙的最大距离Sm?此时倾角α与β各为多大?
分析 (1)对AB过程由动能定理可求得小球的初速度,再由竖直方向的末速度可求得时间;
(2)由平抛运动的规律可求得对应的函数关系,并由斜率求得高度;
(3)根据(2)中求出的关系,由数学规律可求得最大距离.
解答 解:(1)对AB段运用动能定理:$\frac{1}{2}$mv02=mgLsinα
解得:v0=$\sqrt{2gLsinα}$
t=$\frac{{v}_{0}cotβ}{g}$=$\frac{\sqrt{2gLsinα}cotβ}{g}$
(2)设小球平抛过程中水平方向和竖直方向的位移分别为x,y
在空中水平距离x=v0t=2Lsinαcotβ
在空中竖直距离y=$\frac{{v}_{y}^{2}}{2g}$=$\frac{{v}_{0}^{2}co{t}^{2}β}{2g}$=Lsinαcos2β
由$\frac{h-y}{x}=tanβ$,得
cot2β=$\frac{h}{L}(\frac{1}{sinα})-2$,
得到关于$\frac{1}{sinα}$与cot2β的关系式,对应图象横轴表示,对应图象横轴表示$\frac{1}{sinα}$
斜率为$\frac{h}{L}$,由图象可知斜率为2,故$\frac{h}{L}$=2,h=1m;
(3)由第(2)问中x=v0t=sinαcotβ和cot2β=$\frac{h}{L}(\frac{1}{sinα})-2$,
x=$\sqrt{2sinα-2si{n}^{2}α}$
当sinα=$\frac{1}{2}$时,Smax=$\frac{\sqrt{2}}{2}$,此时α=30°
对应β=arccot$\sqrt{2}$=35.3°
答:(1)小球的飞行时间为$\frac{\sqrt{2gLsinα}cotβ}{g}$;
(2)此坐标系的横轴表示$\frac{1}{sinα}$;竖直墙BC的高度h为1m;
(3)小球在CD上的落点离竖直墙的最大距离Sm为$\frac{\sqrt{2}}{2}$;此时倾角α为30°β为35.3°.
点评 本题考查平抛运动及动能定理的规律,难点在于数学知识的应用,要注意根据物理规律结合几何关系进行分析求解.

| A. | 3倍 | B. | 2倍 | C. | 6倍 | D. | 9倍 |
 两电荷量分别为q1和q2的点电荷放在x轴上的O、M两点,两电荷连线上各点电势φ随x变化的关系如图所示,其中A、N两点的电势为零,ND段中C点电势最高,则下列说法不正确的是( )
两电荷量分别为q1和q2的点电荷放在x轴上的O、M两点,两电荷连线上各点电势φ随x变化的关系如图所示,其中A、N两点的电势为零,ND段中C点电势最高,则下列说法不正确的是( )| A. | |q1|<|q2| | |
| B. | q1带正电,q2带负电 | |
| C. | C点的电场强度大小为零 | |
| D. | 将一负点电荷从N点移到D点,电场力先做正功后做负功 |
| A. | 可能是重力对物体做了功 | B. | 一定是合外力对物体做了功 | ||
| C. | 一定是拉力对物体做了功 | D. | 可能是摩擦力对物体做了功 |
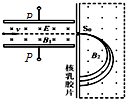 1922年英国物理学家阿斯顿因质谱仪的发明、同位素和质谱仪的研究荣获了诺贝尔化学奖.若一束粒子(不计重力)由左端射入质谱仪后的运动轨迹如图所示,则下列说法正确的是( )
1922年英国物理学家阿斯顿因质谱仪的发明、同位素和质谱仪的研究荣获了诺贝尔化学奖.若一束粒子(不计重力)由左端射入质谱仪后的运动轨迹如图所示,则下列说法正确的是( )| A. | 该束带电粒子带负电 | |
| B. | 速度选择器的上极板带负电 | |
| C. | 在磁场B2中运动半径越大的粒子,质量越大 | |
| D. | 在磁场B2中运动半径越大的粒子,比荷q/m越小 |
| A. | 加速度逐渐减小,而速度逐渐增大 | |
| B. | 加速度方向不变,而速度的方向改变 | |
| C. | 加速度大小不变,方向改变,而速度保持不变 | |
| D. | 物体在运动,而加速度(不为零)和速度都保持不变 |
 某同学为验证系统机械能守恒定律,采用如图所示的实验装置.将气垫导轨调节水平后在上面放上A、B两个光电门,滑块通过一根细线与小盘相连.测得滑块质量M,小盘和砝码的总质量m,滑块上固定的挡光片宽度为d.实验中,静止释放滑块后测得滑块通过光电门A的时间为△tA,通过光电门B的时间为△tB.
某同学为验证系统机械能守恒定律,采用如图所示的实验装置.将气垫导轨调节水平后在上面放上A、B两个光电门,滑块通过一根细线与小盘相连.测得滑块质量M,小盘和砝码的总质量m,滑块上固定的挡光片宽度为d.实验中,静止释放滑块后测得滑块通过光电门A的时间为△tA,通过光电门B的时间为△tB.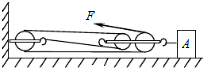 如图所示,滑轮组拉着物体A在水平面上做匀速直线运动.已知mA=500kg,F=612.5N,滑轮组的机械效率η=80%.
如图所示,滑轮组拉着物体A在水平面上做匀速直线运动.已知mA=500kg,F=612.5N,滑轮组的机械效率η=80%.