题目内容
11.某星球的质量是M,半径为R,万有引力常量是G,则该表面的自由落体加速度是$\frac{GM}{{R}^{2}}$,在该星球表面发射一颗卫星,这颗卫星绕星球运行的周期是$\sqrt{\frac{4{π}^{2}{R}^{3}}{GM}}$.分析 根据万有引力等于重力求出星球表面的重力加速度,结合引力提供向心力,即可求解周期.
解答 解:根据万有引力等于重力得,G$\frac{Mm}{{R}^{2}}$=mg,
解得:g=$\frac{GM}{{R}^{2}}$
根据引力提供向心力,则有:$\frac{GMm}{{R}^{2}}=m\frac{4{π}^{2}R}{{T}^{2}}$;
解得:T=$\sqrt{\frac{4{π}^{2}{R}^{3}}{GM}}$
故答案为:$\frac{GM}{{R}^{2}}$,$\sqrt{\frac{4{π}^{2}{R}^{3}}{GM}}$.
点评 解决本题的关键掌握万有引力的两个理论,1、万有引力提供向心力,2、万有引力等于重力.并能灵活运用.

练习册系列答案
相关题目
2.关于冲量、动量与动量变化的下述说法中正确的是( )
| A. | 物体的动量等于物体所受的重力的冲量 | |
| B. | 物体所受合外力的冲量大小等于物体动量的变化大小 | |
| C. | 物体所受合外力的冲量方向与物体动量的变化方向相同 | |
| D. | 物体的动量变化方向一定与物体的初动量方向相同 |
6.以下实例中运动物体机械能一定守恒的是( )
| A. | 物体做匀变速直线运动 | B. | 物体做匀速直线运动 | ||
| C. | 物体做自由落体运动 | D. | 物体做匀速圆周运动 |
3.质量为60kg的人,站在升降机内的台秤上,测得体重为480N,则升降机的运动应是( )
| A. | 匀速上升或匀速下降 | B. | 加速上升或加速下降 | ||
| C. | 减速上升或加速下降 | D. | 减速下降或加速上升 |
20.只在电场力的作用下( )
| A. | 正电荷只能向电势低处运动 | |
| B. | 负电荷只能向电势低处运动 | |
| C. | 电荷在电场线越密集的地方运动越快 | |
| D. | 电荷可能在等势面上运动 |
 n个完全相同的木块并列地放在水平地面上,如图所示.已知木块质量为m,木块与地面间的动摩擦因数为μ.当木块1受到水平力F的作用向前做匀加速运动时,木块3对木块4的作用力大小为:F′=$\frac{(n-3)F}{n}$..
n个完全相同的木块并列地放在水平地面上,如图所示.已知木块质量为m,木块与地面间的动摩擦因数为μ.当木块1受到水平力F的作用向前做匀加速运动时,木块3对木块4的作用力大小为:F′=$\frac{(n-3)F}{n}$.. 如图所示,质量为m=0.01kg的子弹以速度v0=500m/s沿水平方向击中放在直杆顶端的小球,并穿过球心落在地面上.已知h=5.0m,小球质量为M=0.2kg,小球落地处离杆的距离为S=20m,求:
如图所示,质量为m=0.01kg的子弹以速度v0=500m/s沿水平方向击中放在直杆顶端的小球,并穿过球心落在地面上.已知h=5.0m,小球质量为M=0.2kg,小球落地处离杆的距离为S=20m,求: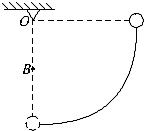 把一个小球用细线悬挂起来,就成为一个摆,如图所示,摆长为L,现将悬线拉至水平后,无初速的释放小球,如果空气阻力不计,求
把一个小球用细线悬挂起来,就成为一个摆,如图所示,摆长为L,现将悬线拉至水平后,无初速的释放小球,如果空气阻力不计,求 如图所示,是沿绳向右传播的一列横波,此刻.
如图所示,是沿绳向右传播的一列横波,此刻.