题目内容
10. 质量为m的A球和质量为3m的B球分别用长为L的细线a和b悬挂在天花板下方,两球恰好相互接触.用细线c水平拉起A,使a偏离竖直方向θ=60°,静止在如图7所示的位置.剪断c,让A 自由摆动下落,重力加速度为g.
质量为m的A球和质量为3m的B球分别用长为L的细线a和b悬挂在天花板下方,两球恰好相互接触.用细线c水平拉起A,使a偏离竖直方向θ=60°,静止在如图7所示的位置.剪断c,让A 自由摆动下落,重力加速度为g.①求A与B发生碰撞前瞬间的速度大小.
②若A与B发生弹性碰撞,求碰后瞬间B的速度大小.
分析 ①剪断c,小球A向下摆过程中,绳子的拉力不做功,其机械能守恒,由机械能守恒定律求出A与B发生碰撞前瞬间的速度大小;
②A与B发生弹性碰撞,根据动量守恒和动能守恒结合求出碰后瞬间B的速度大小.
解答 解:①设A球到达最低点时速度为v,由机械能守恒定律:
mgL(1-cosθ)=$\frac{1}{2}$mv2
解得:v=$\sqrt{gL}$
(2)A与B碰后瞬间,A的速度为vA、B的速度为vB,依题意,A与B发生弹性碰撞,取向左为正方向,根据动量守恒定律和动能守恒得:
mv=mvA+3mvB…①
$\frac{1}{2}$mv2=$\frac{1}{2}$mvA2+$\frac{1}{2}$×3mvB2 …②
由①②解得:vB=$\frac{\sqrt{gL}}{2}$
答:①A与B发生碰撞前瞬间的速度大小为$\sqrt{gL}$.
②若A与B发生弹性碰撞,碰后瞬间B的速度大小为$\frac{\sqrt{gL}}{2}$.
点评 该题涉及多个物理过程,关键要把握每个过程遵守的物理规律,知道弹性碰撞,遵守动量守恒定律和能量守恒定律,列式时要注意选取正方向.

练习册系列答案
相关题目
20. 两颗相距足够远的行星a、b,半径均为R0,两行星各自周围卫星的公转速度的平方v2与公转半径的倒数$\frac{1}{r}$的关系图象如图所示.则关于两颗行星及它们的卫星的描述,正确的是( )
两颗相距足够远的行星a、b,半径均为R0,两行星各自周围卫星的公转速度的平方v2与公转半径的倒数$\frac{1}{r}$的关系图象如图所示.则关于两颗行星及它们的卫星的描述,正确的是( )
 两颗相距足够远的行星a、b,半径均为R0,两行星各自周围卫星的公转速度的平方v2与公转半径的倒数$\frac{1}{r}$的关系图象如图所示.则关于两颗行星及它们的卫星的描述,正确的是( )
两颗相距足够远的行星a、b,半径均为R0,两行星各自周围卫星的公转速度的平方v2与公转半径的倒数$\frac{1}{r}$的关系图象如图所示.则关于两颗行星及它们的卫星的描述,正确的是( )| A. | 行星a的质量较大 | |
| B. | 行星a的第一宇宙速度较大 | |
| C. | 取相同公转半径,行星a的卫星向心加速度较小 | |
| D. | 取相同公转速度,行星a的卫星周期较小 |
15.2015年5月11日,第六届全国特殊奥林匹克运动会在四川开幕,此次是首次将残运会和特奥会合并举办,运动会包括田径、体操、柔道等比赛,下列几种比赛项目中的研究对象可视为质点的是( )
| A. | 在撑杆跳比赛中研究运动员手中的支撑杆在支撑地面过程中的转动情况时 | |
| B. | 帆船比赛中确定帆船在大海中的动作时 | |
| C. | 柔道比赛中确定运动员的动作时 | |
| D. | 铅球比赛中研究铅球被掷出后在空中的飞行时间时 |
2.如图所示为A和B两质点的位移-时间图象,以下说法中正确的是 ( )


| A. | 当t=0时,A、B两质点的速度均为零 | B. | 在运动过程中,A质点运动得比B快 | ||
| C. | 当t=t1时,两质点的位移相等 | D. | 当t=t1时,两质点的速度大小相等 |
 如图所示,小滑块在较长的固定斜面顶端,以初速度v0=2m/s、加速度a=2m/s2沿斜面加速向下滑行,在到达斜面底端前1s内,滑块所滑过的距离为$\frac{7}{15}$L,其中L为斜面长.求滑块在斜面上滑行的时间t和斜面的长度L.
如图所示,小滑块在较长的固定斜面顶端,以初速度v0=2m/s、加速度a=2m/s2沿斜面加速向下滑行,在到达斜面底端前1s内,滑块所滑过的距离为$\frac{7}{15}$L,其中L为斜面长.求滑块在斜面上滑行的时间t和斜面的长度L. 如图所示,一质量为M=1kg的物块静止在桌面边缘,桌面离水平地面的高度为h=1.8m.一质量为m=10g的子弹以水平速度400m/s射入物块后,以水平速度200m/s射出.重力加速度为g=10m/s2.求:
如图所示,一质量为M=1kg的物块静止在桌面边缘,桌面离水平地面的高度为h=1.8m.一质量为m=10g的子弹以水平速度400m/s射入物块后,以水平速度200m/s射出.重力加速度为g=10m/s2.求:
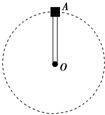 长L=0.5m的轻杆,其一端连接着一个零件A,A的质量m=2kg.现让A在竖直平面内绕O点做匀速圆周运动,如图所示.在A通过最高点时,求下列两种情况下A对杆的作用力大小(g=10m/s2):
长L=0.5m的轻杆,其一端连接着一个零件A,A的质量m=2kg.现让A在竖直平面内绕O点做匀速圆周运动,如图所示.在A通过最高点时,求下列两种情况下A对杆的作用力大小(g=10m/s2):