题目内容
3. 如图所示,一质量为m的小球用细线悬挂起来,就成为一个摆,已知球心到悬点的距离为l,先让小球从偏角θ处由静止释放,如果阻力可以忽略,重力加速度为g,求:
如图所示,一质量为m的小球用细线悬挂起来,就成为一个摆,已知球心到悬点的距离为l,先让小球从偏角θ处由静止释放,如果阻力可以忽略,重力加速度为g,求:(1)小球运动到最低点时的速度大小v;
(2)小球运动到最低点时细线的拉力大小F.
分析 (1)对小球由最高点运动到最低点过程根据动能定理即可求得小球到达最低点时的速度大小;
(2)小球做圆周运动,最低点处拉力和重力的合力提供向心力,根据向心力公式即可求得细线的拉力大小.
解答 解:(1)对小球摆到最低点的过程,根据动能定理可知:
mgl(1-cosθ)=$\frac{1}{2}$mv2-0
解得:v=$\sqrt{2gl(1-cosθ)}$
(2)在最低点小球受拉力和重力作用,根据向心力公式可得:
F-mg=m$\frac{{v}^{2}}{l}$
解得:F=3mg-2mgcosθ.
答:(1)小球运动到最低点时的速度大小v为$\sqrt{2gl(1-cosθ)}$;
(2)小球运动到最低点时细线的拉力大小F为3mg-2mgcosθ.
点评 本题综合考查了动能定理和牛顿第二定律,要注意正确分析物理过程,明确物体规律的应用,注意和一问也可以根据机械能守恒列式计算.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13. 如图所示,水平地面上固定一倾角为θ的光滑斜面,斜面顶端固定一轻质弹簧,弹簧另一端与A球相连,三个完全相同的小球A、B、C静止在斜面上,A、B、C间均由一轻质细线连接,弹簧与细线均平行于斜面,A、B间细线被烧断的瞬间(重力加速度为g),下列说法正确的是( )
如图所示,水平地面上固定一倾角为θ的光滑斜面,斜面顶端固定一轻质弹簧,弹簧另一端与A球相连,三个完全相同的小球A、B、C静止在斜面上,A、B、C间均由一轻质细线连接,弹簧与细线均平行于斜面,A、B间细线被烧断的瞬间(重力加速度为g),下列说法正确的是( )
 如图所示,水平地面上固定一倾角为θ的光滑斜面,斜面顶端固定一轻质弹簧,弹簧另一端与A球相连,三个完全相同的小球A、B、C静止在斜面上,A、B、C间均由一轻质细线连接,弹簧与细线均平行于斜面,A、B间细线被烧断的瞬间(重力加速度为g),下列说法正确的是( )
如图所示,水平地面上固定一倾角为θ的光滑斜面,斜面顶端固定一轻质弹簧,弹簧另一端与A球相连,三个完全相同的小球A、B、C静止在斜面上,A、B、C间均由一轻质细线连接,弹簧与细线均平行于斜面,A、B间细线被烧断的瞬间(重力加速度为g),下列说法正确的是( )| A. | A球的加速度沿斜面向上,大小为3gsinθ | |
| B. | B球的加速度沿斜面向下,大小为gsinθ | |
| C. | B球的加速度沿斜面向下,大小为2gsinθ | |
| D. | C球的加速度沿斜面向下,大小为gsinθ |
14. 完全相同的两物体P、Q,质量均为m,叠放在一起置于水平面上,如图所示.现用两根等长的细线系在两物体上,两细绳间的夹角为120°,在细线的结点处施加一水平拉力F,两物体始终保持静止状态,则下列说法正确的是(重力加速度为g)( )
完全相同的两物体P、Q,质量均为m,叠放在一起置于水平面上,如图所示.现用两根等长的细线系在两物体上,两细绳间的夹角为120°,在细线的结点处施加一水平拉力F,两物体始终保持静止状态,则下列说法正确的是(重力加速度为g)( )
 完全相同的两物体P、Q,质量均为m,叠放在一起置于水平面上,如图所示.现用两根等长的细线系在两物体上,两细绳间的夹角为120°,在细线的结点处施加一水平拉力F,两物体始终保持静止状态,则下列说法正确的是(重力加速度为g)( )
完全相同的两物体P、Q,质量均为m,叠放在一起置于水平面上,如图所示.现用两根等长的细线系在两物体上,两细绳间的夹角为120°,在细线的结点处施加一水平拉力F,两物体始终保持静止状态,则下列说法正确的是(重力加速度为g)( )| A. | 物体P受到细线的拉力大小为F | B. | 两物体间弹力大小可能为mg+$\frac{F}{2}$ | ||
| C. | 两物体间的摩擦力大小为F | D. | 地面对Q的摩擦力为F |
11. 如图所示为一种早期发电机的原理示意图,该发电机由固定的圆形线圈和一对用铁芯连接的圆柱形磁铁构成,两磁极相对于线圈平面对称.当磁极绕转轴匀速转动时,磁极中心在线圈平面上的投影沿圆弧MOP运动(O是线圈的中心).在磁极的投影从M点运动到P点的过程中( )
如图所示为一种早期发电机的原理示意图,该发电机由固定的圆形线圈和一对用铁芯连接的圆柱形磁铁构成,两磁极相对于线圈平面对称.当磁极绕转轴匀速转动时,磁极中心在线圈平面上的投影沿圆弧MOP运动(O是线圈的中心).在磁极的投影从M点运动到P点的过程中( )
 如图所示为一种早期发电机的原理示意图,该发电机由固定的圆形线圈和一对用铁芯连接的圆柱形磁铁构成,两磁极相对于线圈平面对称.当磁极绕转轴匀速转动时,磁极中心在线圈平面上的投影沿圆弧MOP运动(O是线圈的中心).在磁极的投影从M点运动到P点的过程中( )
如图所示为一种早期发电机的原理示意图,该发电机由固定的圆形线圈和一对用铁芯连接的圆柱形磁铁构成,两磁极相对于线圈平面对称.当磁极绕转轴匀速转动时,磁极中心在线圈平面上的投影沿圆弧MOP运动(O是线圈的中心).在磁极的投影从M点运动到P点的过程中( )| A. | 流过电流表的电流由F指向E | |
| B. | 流过电流表的电流先增大再减小 | |
| C. | 流过电流表的电流先增大再减小,然后再增大、再减小 | |
| D. | 流过电流表的电流先减小再增大 |
18. 在两个足够长的固定的相同斜面体上(其斜面光滑),分别有如图所示的两套装置(斜面体B的上表面水平且光滑、长方体D的上表面与斜面平行且光滑,p是固定在B、D上的小柱,完全相同的两只弹簧一端固定在p上,另一端分别连在A和C上,在A与B、C与D分别保持相对静止状态沿斜面自由下滑的过程中,下列说法正确的是( )
在两个足够长的固定的相同斜面体上(其斜面光滑),分别有如图所示的两套装置(斜面体B的上表面水平且光滑、长方体D的上表面与斜面平行且光滑,p是固定在B、D上的小柱,完全相同的两只弹簧一端固定在p上,另一端分别连在A和C上,在A与B、C与D分别保持相对静止状态沿斜面自由下滑的过程中,下列说法正确的是( )
 在两个足够长的固定的相同斜面体上(其斜面光滑),分别有如图所示的两套装置(斜面体B的上表面水平且光滑、长方体D的上表面与斜面平行且光滑,p是固定在B、D上的小柱,完全相同的两只弹簧一端固定在p上,另一端分别连在A和C上,在A与B、C与D分别保持相对静止状态沿斜面自由下滑的过程中,下列说法正确的是( )
在两个足够长的固定的相同斜面体上(其斜面光滑),分别有如图所示的两套装置(斜面体B的上表面水平且光滑、长方体D的上表面与斜面平行且光滑,p是固定在B、D上的小柱,完全相同的两只弹簧一端固定在p上,另一端分别连在A和C上,在A与B、C与D分别保持相对静止状态沿斜面自由下滑的过程中,下列说法正确的是( )| A. | 两弹簧都处于拉伸状态 | |
| B. | 两弹簧都处于压缩状态 | |
| C. | 弹簧L1处于压缩状态,弹簧L2处于原长 | |
| D. | 弹簧L1处于拉伸状态,弹簧L2处于压缩状态 |
7. 如图所示,正沿平直轨道向右匀速行驶的车厢内,用水平绳a和倾斜绳b共同固定一个小球,若车厢改做加速运动,则两绳的拉力FTa和FTb的变化情况是( )
如图所示,正沿平直轨道向右匀速行驶的车厢内,用水平绳a和倾斜绳b共同固定一个小球,若车厢改做加速运动,则两绳的拉力FTa和FTb的变化情况是( )
 如图所示,正沿平直轨道向右匀速行驶的车厢内,用水平绳a和倾斜绳b共同固定一个小球,若车厢改做加速运动,则两绳的拉力FTa和FTb的变化情况是( )
如图所示,正沿平直轨道向右匀速行驶的车厢内,用水平绳a和倾斜绳b共同固定一个小球,若车厢改做加速运动,则两绳的拉力FTa和FTb的变化情况是( )| A. | FTa增大 | B. | FTb减小 | ||
| C. | FTa不变 | D. | FTa、FTb的合力增大 |
13.某电场中电场线的分布如图所示,下列说法正确的是( )


| A. | B点的电势高 | |
| B. | B点的场强大 | |
| C. | 同一试探电荷在A点的加速度大于在B点的加速度 | |
| D. | 电荷在A点受力方向一定与A点场强方向一致 |

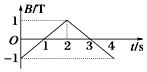 一个边长为10cm的正方形金属线框置于匀强磁场中,线框匝数n=100,线框平面与磁场垂直,电阻为20Ω.磁感应强度随时间变化的图象如图所示.则前两秒产生的电动势为1 V.
一个边长为10cm的正方形金属线框置于匀强磁场中,线框匝数n=100,线框平面与磁场垂直,电阻为20Ω.磁感应强度随时间变化的图象如图所示.则前两秒产生的电动势为1 V.