题目内容
18.如图(a)所示,在水平光滑轨道上停着甲、乙两辆实验小车,甲车系一穿过打点计时器的纸带,当甲车受到水平向右的冲量后,随即启动打点计时器,甲车运动一段距离后,与静止的乙车正碰并黏在一起运动,纸带记录下碰撞前甲车和碰撞后两车运动情况如图(b)所示,电源频率为50Hz.则:碰撞前甲车运动速度大小为0.6m/s,甲、乙两车的质量比m甲:m乙为2:1.
分析 由纸带所示数据求出碰前甲车速度与碰撞后两车的共同速度;碰撞过程中,两车组成的系统动量守恒,由动量守恒定律可以求出两车质量之比.
解答 解:碰前甲做匀速运动,由纸带可求得甲车碰前的速度为:v1=$\frac{{s}_{1}}{T}$=$\frac{0.12}{0.02}$=0.6m/s,
碰后甲、乙一起做运动运动,速度:v2=$\frac{{s}_{2}}{T}$=$\frac{0.008}{0.02}$=0.4m/s,
以向右为正方向,由动量守恒定律得 m甲v1=(m甲+m乙)v2,
甲、乙两车质量之比为$\frac{{m}_{甲}}{{m}_{乙}}$=$\frac{{v}_{2}}{{v}_{1}-{v}_{2}}$=$\frac{0.4}{0.6-0.4}$=$\frac{2}{1}$;
故答案为:0.6;2:1.
点评 由纸带数据应用速度公式求出车的速度、应用动量守恒定律即可正确解题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
6.关于物体的运动状态下列说法正确的是( )
| A. | 速度小的物体,运动状态易于改变 | |
| B. | 做曲线运动的物体,运动状态一定会发生变化 | |
| C. | 做直线运动的物体,运动状态一定不发生变化 | |
| D. | 做自由落体运动的物体,运动状态不发生变化 |
13. 在“验证牛顿第二定律”的实验中,某同学做出的a-$\frac{1}{M}$的关系图线,如图所示.从图象中可以看出,作用在物体上的恒力F=5N.当物体的质量为2.5kg时,它的加速度为2m/s2.
在“验证牛顿第二定律”的实验中,某同学做出的a-$\frac{1}{M}$的关系图线,如图所示.从图象中可以看出,作用在物体上的恒力F=5N.当物体的质量为2.5kg时,它的加速度为2m/s2.
 在“验证牛顿第二定律”的实验中,某同学做出的a-$\frac{1}{M}$的关系图线,如图所示.从图象中可以看出,作用在物体上的恒力F=5N.当物体的质量为2.5kg时,它的加速度为2m/s2.
在“验证牛顿第二定律”的实验中,某同学做出的a-$\frac{1}{M}$的关系图线,如图所示.从图象中可以看出,作用在物体上的恒力F=5N.当物体的质量为2.5kg时,它的加速度为2m/s2.
3.如图所示,闭合开关S后,当滑动变阻器的滑片P向上端a滑动时,两表的示数将( )
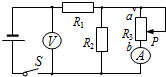

| A. | 电压表示数增大 | B. | 电压表示数减小 | C. | 电流表示数增大 | D. | 电流表示数减小 |
10.如图所示电路中,已知I1=3mA,I2=1mA,则电路元件3中的电流和其两端电压分别为( )


| A. | 2mA 60V | B. | -2mA 60V | C. | -2mA-60V | D. | 2mA-60V |
7. 如图所示,质量为m的光滑小球置于斜面上,被一个竖直固定在斜面上的挡板挡住.现使斜面在水平面上向右做加速度为a的匀加速直线运动,下列法中正确的是( )
如图所示,质量为m的光滑小球置于斜面上,被一个竖直固定在斜面上的挡板挡住.现使斜面在水平面上向右做加速度为a的匀加速直线运动,下列法中正确的是( )
 如图所示,质量为m的光滑小球置于斜面上,被一个竖直固定在斜面上的挡板挡住.现使斜面在水平面上向右做加速度为a的匀加速直线运动,下列法中正确的是( )
如图所示,质量为m的光滑小球置于斜面上,被一个竖直固定在斜面上的挡板挡住.现使斜面在水平面上向右做加速度为a的匀加速直线运动,下列法中正确的是( )| A. | 若加速度足够小,竖直挡板对球的弹力可能为零 | |
| B. | 若加速度足够大,斜面对球的弹力可能为零 | |
| C. | 斜面和挡板对球的弹力的合力大于ma | |
| D. | 加速度由a增大至2a的过程中,斜面对球的弹力增大 |
8.下列说法中正确的是( )
| A. | 跳高运动员起跳,人对地的压力大于地对人的支持力 | |
| B. | 钢丝绳吊起货物加速上升时,钢丝绳对货物的拉力等于货物对钢丝绳的拉力 | |
| C. | 火箭加速上升时,火箭发动机的推力大于火箭的重力 | |
| D. | 以鸡蛋撞石头,鸡蛋破碎,石头对鸡蛋的力大于鸡蛋对石头的力 |
 如图是直流电动机的原理图,其中P、Q和X、Y是电动机中的两个部件,电动机中的转子能够不停地绕同一方向转动,是利用上述部件中X、Y部件实现的,我们把这一部件叫做换向器.
如图是直流电动机的原理图,其中P、Q和X、Y是电动机中的两个部件,电动机中的转子能够不停地绕同一方向转动,是利用上述部件中X、Y部件实现的,我们把这一部件叫做换向器.