题目内容
12. 电子从静止开始经U1=45V电压的加速电场加速,然后垂直电场方向从平行板正中央进入电压U2=280V的偏转电场,恰好打在下极板中央.已知电子质量m=0.9×10-30千克,电荷量q=1.6×10-19C.(不记记电子重力)
电子从静止开始经U1=45V电压的加速电场加速,然后垂直电场方向从平行板正中央进入电压U2=280V的偏转电场,恰好打在下极板中央.已知电子质量m=0.9×10-30千克,电荷量q=1.6×10-19C.(不记记电子重力)求:(1)电子进入偏转电场时的速度;
(2)保持其它条件不变,若要电子飞出电场,偏转电场电压达满足什么条件?
(3)在满足上问的条件下,电子飞出偏转电场的最大速度?
分析 (1)根据动能定理求出电子经U1加速后的速度v0.即为电子进入偏转电场时的速度.
(2)电子进入偏转电场后做类平抛运动,将类平抛分解,在水平方向上做匀速直线运动,竖直方向上做初速度为零的匀加速直线运动.电子恰好打在下极板中央时,水平位移为板长一半,竖直位移等于板间距离的一半.当电子恰好飞出电场时,水平位移等于板长,竖直位移等于板间距离的一半.对两种情况,分别列出分位移表达式,再求解.
(3)电场力做功最大时电子飞出电场时速度最大,由动能定理求解.
解答 解:(1)电子在加速电场中运动过程,由动能定理得
eU1=$\frac{1}{2}$mv02;
得 v0=$\sqrt{\frac{2e{U}_{1}}{m}}$=$\sqrt{\frac{2×1.6×1{0}^{-19}×45}{0.9×1{0}^{-30}}}$=4×106m/s
故电子进入偏转电场时的速度 v0=4×106m/s
(2)设右侧金属板长为L,板间距离为d.电子恰好飞出电场时,偏转电场电压为U3.
当电子恰好打在下极板中央时,有
$\frac{L}{2}$=v0t
$\frac{d}{2}$=$\frac{1}{2}a{t}^{2}$
又 a=$\frac{e{U}_{2}}{md}$
联立得 U2=$\frac{4m{d}^{2}{v}_{0}^{2}}{e{L}^{2}}$
当电子恰好飞出电场时,有
L=v0t′
$\frac{d}{2}$=$\frac{1}{2}a′t{′}^{2}$
又 a′=$\frac{e{U}_{3}}{md}$
联立得 U3=$\frac{m{d}^{2}{v}_{0}^{2}}{e{L}^{2}}$
对比可得,U3=$\frac{1}{4}$U2=70V
所以,若要电子飞出电场,偏转电场电压应满足的条件是:U2<70V.
(3)电子恰好飞出电场时,电场力做功最大,电子飞出电场时速度最大,对整个过程,由动能定理得:
eU1+e•$\frac{{U}_{3}}{2}$=$\frac{1}{2}m{v}^{2}$
解得,电子飞出偏转电场的最大速度为 v=$\frac{16}{3}$×106m/s
答:
(1)电子进入偏转电场时的速度是4×106m/s;
(2)保持其它条件不变,若要电子飞出电场,偏转电场电压的条件是:U2<70V.
(3)在满足上问的条件下,电子飞出偏转电场的最大速度是$\frac{16}{3}$×106m/s.
点评 解决本题的关键对类平抛运动进行分解,抓住两分运动具有等时性,运用牛顿第二定律和运动学公式结合处理.

 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案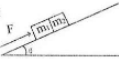 如图足够长的光滑斜面上,用平行于斜面向上的恒力F推m1,使m1、m2向上加速运动,m1与m2之间的接触面与斜面垂直,斜面倾角用θ表示,质量m1≠m2,则( )
如图足够长的光滑斜面上,用平行于斜面向上的恒力F推m1,使m1、m2向上加速运动,m1与m2之间的接触面与斜面垂直,斜面倾角用θ表示,质量m1≠m2,则( )| A. | m1与m2之间弹力大小与θ有关 | |
| B. | m1与m2向上运动的加速度大小既与F有关,也与θ有关 | |
| C. | 若某时刻撤去F,则该时刻m1与m2即将分离 | |
| D. | 若改用同样大小的力平行于斜面向下推m2,使m1与m2一起向下加速运动,则m1与m2之间的弹力大小改变 |
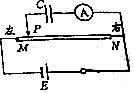 如图所示,E为内阻不计的电源,MN为同种材料制成的粗细均匀的长电阻丝,C为电容器.当滑动触头P以恒定速率从左向右匀速滑动时,关于电流计A的读数情况及通过A的电流方向.下列说法正确的是( )
如图所示,E为内阻不计的电源,MN为同种材料制成的粗细均匀的长电阻丝,C为电容器.当滑动触头P以恒定速率从左向右匀速滑动时,关于电流计A的读数情况及通过A的电流方向.下列说法正确的是( )| A. | 读数逐渐变小.通过A的电流方向向左 | |
| B. | 读数逐渐变大,通过A的电流方向向右 | |
| C. | 读数稳定,通过A的电流方向向右 | |
| D. | 读数稳定,通过A的电流方向向左 |
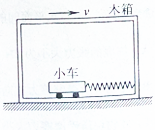 如图所示,质量为2kg的木箱以2m/s2的加速度水平向右做匀加速运动,在箱内有一劲度系数为50N/m的轻弹簧,其一被固定在箱子的右侧壁,另一端拴接一个质量为1kg的小车,木箱与小车相对静止,如图所示.不计小车与木箱之间的摩擦,则( )
如图所示,质量为2kg的木箱以2m/s2的加速度水平向右做匀加速运动,在箱内有一劲度系数为50N/m的轻弹簧,其一被固定在箱子的右侧壁,另一端拴接一个质量为1kg的小车,木箱与小车相对静止,如图所示.不计小车与木箱之间的摩擦,则( )| A. | 弹簧被压缩8cm | B. | 弹簧被压缩4cm | C. | 弹簧被拉伸8cm | D. | 弹簧被拉伸4cm |
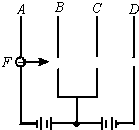 如图所示,从P处释放一个无初速度的电子向B板方向运动,指出下列对电子运动的描述中哪项是正确的(设电源电动势E)( )
如图所示,从P处释放一个无初速度的电子向B板方向运动,指出下列对电子运动的描述中哪项是正确的(设电源电动势E)( )| A. | 电子到达B板时的动能是Ee | B. | 电子从B板到达C板动能变化量为零 | ||
| C. | 电子到达D板时动能是2Ee | D. | 电子在A板和D板之间做往复运动 |
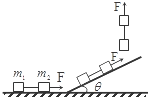 如图所示,质量为m1和m2的两个材料相同的物体用细线相连,在大小恒定的拉力F作用下,先沿水平面,再沿斜面,最后竖直向上匀加速运动,不计空气阻力,在三个阶段的运动中,线上拉力的大小( )
如图所示,质量为m1和m2的两个材料相同的物体用细线相连,在大小恒定的拉力F作用下,先沿水平面,再沿斜面,最后竖直向上匀加速运动,不计空气阻力,在三个阶段的运动中,线上拉力的大小( )| A. | 由大变小 | B. | 由小变大 | ||
| C. | 始终不变且大小为$\frac{m}{{m}_{1}+{m}_{2}}$F | D. | 由大变小再变大 |
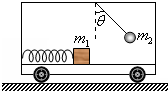 在水平地面上运动的小车车厢底部有一质量为m1的木块,木块和车厢通过一根轻质弹簧相连接,弹簧的劲度系数为k.在车厢的顶部用一根细线悬挂一质量为m2的小球.某段时间内发现细线与竖直方向的夹角为θ,在这段时间内木块与车厢始终保持相对静止,如图所示.不计木块与车厢底部的摩擦力,则在这段时间内弹簧处在拉伸(选填“压缩”或“拉伸”)状态,形变量为$\frac{{{m_1}gtanθ}}{k}$.
在水平地面上运动的小车车厢底部有一质量为m1的木块,木块和车厢通过一根轻质弹簧相连接,弹簧的劲度系数为k.在车厢的顶部用一根细线悬挂一质量为m2的小球.某段时间内发现细线与竖直方向的夹角为θ,在这段时间内木块与车厢始终保持相对静止,如图所示.不计木块与车厢底部的摩擦力,则在这段时间内弹簧处在拉伸(选填“压缩”或“拉伸”)状态,形变量为$\frac{{{m_1}gtanθ}}{k}$.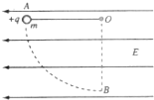 如图所示,空间某区域存在水平方向的匀强电场E=2×104N/C,将一长为L=500cm的不可伸长的绝缘细线一端固定于O点,另一端连接一个质量为m=0.5kg的小球(可视为质点),小球带电量q=1.6×10-4C,现将绝缘细线AO拉至与电场线平行位置,且细线刚好拉直,让小球从A处静止释放,取g=10m/s2,求:
如图所示,空间某区域存在水平方向的匀强电场E=2×104N/C,将一长为L=500cm的不可伸长的绝缘细线一端固定于O点,另一端连接一个质量为m=0.5kg的小球(可视为质点),小球带电量q=1.6×10-4C,现将绝缘细线AO拉至与电场线平行位置,且细线刚好拉直,让小球从A处静止释放,取g=10m/s2,求: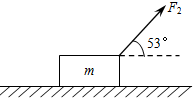 质量m=20kg的木箱放在水平地面上,木箱与地面之间的动摩擦因数μ=0.5.若用水平力F1拉木箱,木箱恰好做匀速直线运动;若用F2=150N、与水平方向成53°斜向上的拉力作用于静止的木箱上,如图所示,作用时间4s后撤去F2.求:
质量m=20kg的木箱放在水平地面上,木箱与地面之间的动摩擦因数μ=0.5.若用水平力F1拉木箱,木箱恰好做匀速直线运动;若用F2=150N、与水平方向成53°斜向上的拉力作用于静止的木箱上,如图所示,作用时间4s后撤去F2.求: