题目内容
18.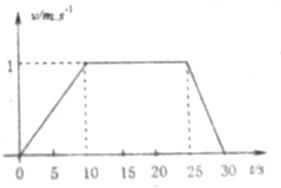 一质量为m=40kg的小孩站在电梯水平地板上,电梯从t=0时刻由静止开始竖直上升,速度随时间变化规律如图所示,取g=10m/s2,求:
一质量为m=40kg的小孩站在电梯水平地板上,电梯从t=0时刻由静止开始竖直上升,速度随时间变化规律如图所示,取g=10m/s2,求:(1)前10s时小孩对电梯的压力多大?
(2)第20s末小孩克服重力的功率多大?
(3)前10s内电梯对小孩做功是多少?
分析 v-t图象的斜率表示加速度,有牛顿第二定律求力,牛顿第三定律求反作用力;由功率公式P=Fv求功率;图象与时间轴包围的面积表示位移大小,根据功的公式求即可.
解答 解:v-t图象与时间轴包围的面积表示位移大小,故在10s内电梯上升的高度是:
H=$\frac{1}{2}$×10×1=5m
加速过程加速度:a=$\frac{1}{10}$=0.1m/s2
根据牛顿第二定律,得:
N-mg=ma1
N=mg+ma1=400+40×0.1=404N
根据牛顿第三定律,得
N′=-N=-404N即
前10s时小孩对电梯的压力为404N
(2)由功率公式P=Fv=mgv=400×1=400W
(3)前10s内的位移图象与时间轴包围的面积x=$\frac{1}{2}$×10×1=5m
电梯对小孩做功是w=N×s=404×5=2020J
答:(1)前10s时小孩对电梯的压力404N(2)第20s末小孩克服重力的功率400W
(3)前10s内电梯对小孩做功是2020J
点评 本题关键是明确物体的运动情况和受力情况,知道v-t图象的斜面和面积的物理意义,然后结合牛顿第二定律列式分析,基础题目

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
9.下列属于反冲运动的是( )
| A. | 汽车的运动 | B. | 直升飞机的运动 | ||
| C. | 火箭的运动 | D. | 反击式水轮机的运动 |
7.关于功率,下列说法正确的是( )
| A. | 由功率P=$\frac{W}{t}$,只要知道W和t的值就可求任意时刻的功率 | |
| B. | 汽车发动机功率达到额定功率,当牵引力等于阻力时,汽车的速度最大 | |
| C. | 由P=F•v可知,当发动机功率一定时,牵引力与速度成正比 | |
| D. | 由P=F•v可知,汽车的功率和它的速度成正比 |
8. 如图所示,ab两条曲线为汽车a、b在同一条平直公路上的速度-时间图象,已知a、b曲线关于它们两交点的连线对称,且在t2时刻两车相遇,下列说法正确的是( )
如图所示,ab两条曲线为汽车a、b在同一条平直公路上的速度-时间图象,已知a、b曲线关于它们两交点的连线对称,且在t2时刻两车相遇,下列说法正确的是( )
 如图所示,ab两条曲线为汽车a、b在同一条平直公路上的速度-时间图象,已知a、b曲线关于它们两交点的连线对称,且在t2时刻两车相遇,下列说法正确的是( )
如图所示,ab两条曲线为汽车a、b在同一条平直公路上的速度-时间图象,已知a、b曲线关于它们两交点的连线对称,且在t2时刻两车相遇,下列说法正确的是( )| A. | 在t1~t2这段时间内,两车位移等大 | |
| B. | 在t1~t2这段时间内的相同时刻,a车与b车的加速度大小有可能不相等 | |
| C. | t1时刻两车也相遇 | |
| D. | t1时刻a车在后,b车在前 |
 如图所示为交流发电机模型,已知n匝线圈的面积为S,在磁感应强度为B的匀强磁场中匀速转动,角速度为ω,线圈电阻为r,负载电阻为R,线圈由图示位围转动90°的过程中,求:
如图所示为交流发电机模型,已知n匝线圈的面积为S,在磁感应强度为B的匀强磁场中匀速转动,角速度为ω,线圈电阻为r,负载电阻为R,线圈由图示位围转动90°的过程中,求: 某村在较远的地方建立了一座小型水电站,发电机的输出功率为100kW,输出电压为500V,输电导线的总电阻为10Ω,导线上损耗的电功率为4kW,该村的用电电压是220V.
某村在较远的地方建立了一座小型水电站,发电机的输出功率为100kW,输出电压为500V,输电导线的总电阻为10Ω,导线上损耗的电功率为4kW,该村的用电电压是220V.