题目内容
9. 如图所示,水平放置的光滑平行金属导轨MN、PQ处于竖直向下的足够大的匀强磁场中,导轨间距为L,导轨右端接有阻值为R的电阻.一根质量为m,电阻为r的金属棒垂直导轨放置,并与导轨接触良好.现使金属棒以某初速度向左运动,它先后经过位置a、b后,到达位置c处刚好静止.已知磁场的磁感应强度为B,金属棒经过a、b处的速度分别为v1、v2,a、b间距离等于b、c间距离,导轨电阻忽略不计.下列说法中正确的是( )
如图所示,水平放置的光滑平行金属导轨MN、PQ处于竖直向下的足够大的匀强磁场中,导轨间距为L,导轨右端接有阻值为R的电阻.一根质量为m,电阻为r的金属棒垂直导轨放置,并与导轨接触良好.现使金属棒以某初速度向左运动,它先后经过位置a、b后,到达位置c处刚好静止.已知磁场的磁感应强度为B,金属棒经过a、b处的速度分别为v1、v2,a、b间距离等于b、c间距离,导轨电阻忽略不计.下列说法中正确的是( )| A. | 金属棒运动到a处时的加速度大小为$\frac{{B}^{2}{L}^{2}{v}_{1}}{mR}$ | |
| B. | 金属棒运动到b处时通过电阻R的电流方向由Q指向N | |
| C. | 金属棒在a→b与b→c过程中通过电阻R的电荷量相等 | |
| D. | 金属棒在a处的速度v1是其在b处速度v2的$\sqrt{2}$倍 |
分析 根据法拉第定律、欧姆定律和安培力公式求出安培力,再由牛顿第二定律求加速度.由右手定则判断感应电流的方向.根据q=$\frac{△Φ}{R+r}$分析电荷量的关系.由于金属棒做变减速运动,可运用动量定理求解v1与v2的关系.
解答 解:A、金属棒运动到a处时,有 E=BLva,I=$\frac{E}{R+r}$,安培力:F=BIL=$\frac{{B}^{2}{L}^{2}{v}_{a}}{R+r}$,由牛顿第二定律得加速度:a=$\frac{F}{m}$=$\frac{{B}^{2}{L}^{2}{v}_{a}}{m(R+r)}$,故A错误.
B、金属棒运动到b处时,由右手定则判断知,通过电阻的电流方向由Q指向N,故B正确.
C、金属棒在a→b过程中,通过电阻的电荷量 q1=$\overline{I}$t=$\frac{\overline{E}}{R+r}$t=$\frac{△Φ{\\;}_{1}}{R+r}$,同理,在b→c的过程中,通过电阻的电荷量 q2=$\frac{△Φ{\\;}_{2}}{R+r}$,由于△Φ1=△Φ2,可得q1=q2.故C正确.
D、在b→c的过程中,对金属棒运用动量定理得:-∑$\frac{{B}^{2}{L}^{2}v}{R+r}$=0-mv2,而∑v△t=lbc,解得:v2=$\frac{{B}^{2}{L}^{2}{l}_{bc}}{m(R+r)}$,同理,在a→c的过程中,对金属棒运用动量定理得:-∑$\frac{{B}^{2}{L}^{2}v}{R+r}$′=0-mv1,而∑v△t′=lac,解得:va=$\frac{{B}^{2}{L}^{2}{l}_{ac}}{m(R+r)}$,因lac=2lbc,因此v1=2v2,故D错误.
故选:BC.
点评 解决本题的关键是推导出安培力表达式、感应电荷量表达式.对于非匀变速运动,研究速度可根据动量定理求解.

 如图所示为交流发电机示意图,线圈的AB边连在金属滑环K上,CD边连在滑环L上,两个电刷E、F分别压在两个滑环上,线圈在转动时可以通过滑环和电刷保持与外电路的连接,下列说法正确的是( )
如图所示为交流发电机示意图,线圈的AB边连在金属滑环K上,CD边连在滑环L上,两个电刷E、F分别压在两个滑环上,线圈在转动时可以通过滑环和电刷保持与外电路的连接,下列说法正确的是( )| A. | 当线圈平面转到中性面的瞬间,穿过线圈的磁通量最小 | |
| B. | 当线圈平面转到跟中性面垂直的瞬间,穿过线圈的磁通量最小 | |
| C. | 当线圈平面转到中性面的瞬间,线圈中的感应电流最大 | |
| D. | 当线圈平面转到跟中性面垂直的瞬间,线圈中的感应电流最小 |
 一细圆环上均匀分布着负电荷,M、N是圆环轴线上的两个点,它们到圆心O的距离$\overline{MO}$>$\overline{NO}$,M、N两点电场强度大小和电势分别用EM,EN和ΦM,ΦN表示,则( )
一细圆环上均匀分布着负电荷,M、N是圆环轴线上的两个点,它们到圆心O的距离$\overline{MO}$>$\overline{NO}$,M、N两点电场强度大小和电势分别用EM,EN和ΦM,ΦN表示,则( )| A. | EM<EN | B. | EM>EN | C. | ΦM<ΦN | D. | ΦM>ΦN |
| A. | 在匀速运动中,存在加速度且加速度大小和方向均不变 | |
| B. | 在匀速运动中,不存在加速度 | |
| C. | 在变速运动中,存在加速度,且加速度变小时,它的速度也随着变小 | |
| D. | 在变速运动中,存在加速度,且加速度不变时,它的速度也不变 |
 如图所示是A、B两物体从同一地点出发运动的x-t图象,图象A是一条直线,图象B是抛物线,则下列说法正确的是( )
如图所示是A、B两物体从同一地点出发运动的x-t图象,图象A是一条直线,图象B是抛物线,则下列说法正确的是( )| A. | 物体 B 做曲线运动 | B. | 物体 B 初速度是 10m/s | ||
| C. | 物体 A 做匀加速直线运动 | D. | t=8s 时,两物体相遇 |
| A. | 亚里士多德 | B. | 伽利略 | C. | 牛顿 | D. | 爱因斯坦 |
 图为某同学改装毫安表的电路图,已知毫安表表头的内阻为100Ω,满偏电流为1mA,R1和R2为阻值固定的电阻.若使用如图电路可以得到量程为3mA和10mA的电流表A1和A2,则:
图为某同学改装毫安表的电路图,已知毫安表表头的内阻为100Ω,满偏电流为1mA,R1和R2为阻值固定的电阻.若使用如图电路可以得到量程为3mA和10mA的电流表A1和A2,则: 如图,某截面为直角三角形的玻璃棱镜ABC,BC边长为L,∠B=90°,∠C=30°,一条光线垂直于AB边E点射入棱镜且AE=$\frac{L}{5}$.光线最终从BC边的中点D射出,出射光线和BC边的夹角θ=45°,光在真空中传播速度为c.
如图,某截面为直角三角形的玻璃棱镜ABC,BC边长为L,∠B=90°,∠C=30°,一条光线垂直于AB边E点射入棱镜且AE=$\frac{L}{5}$.光线最终从BC边的中点D射出,出射光线和BC边的夹角θ=45°,光在真空中传播速度为c.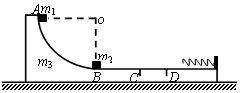 如图所示,质量为m3=2kg的滑道静止在光滑的水平面上,滑道的AB部分是半径为R=1.2m的四分之一圆弧,圆弧底部与滑道水平部分相切,滑道水平部分右端固定一个轻弹簧.滑道除CD部分粗糙外其他部分均光滑.质量为m2=3kg的物体2(可视为质点)放在滑道的B点,现让质量为m1=1kg的物体1(可视为质点)自A点由静止释放.两物体在滑道上的C点相碰后粘为一体(g=10m/s2).求:
如图所示,质量为m3=2kg的滑道静止在光滑的水平面上,滑道的AB部分是半径为R=1.2m的四分之一圆弧,圆弧底部与滑道水平部分相切,滑道水平部分右端固定一个轻弹簧.滑道除CD部分粗糙外其他部分均光滑.质量为m2=3kg的物体2(可视为质点)放在滑道的B点,现让质量为m1=1kg的物体1(可视为质点)自A点由静止释放.两物体在滑道上的C点相碰后粘为一体(g=10m/s2).求: