题目内容
20.某恒星的半径为R,现有一颗行星在距恒星表面高为h的圆形轨道上绕其运动,并测出了运动周期为T,则行星的线速度为$\frac{2π(R+h)}{T}$,恒星的质量为$\frac{4{π}_{\;}^{2}(R+h)_{\;}^{3}}{G{T}_{\;}^{2}}$,恒星的密度为$\frac{3π(R+h)_{\;}^{3}}{G{T}_{\;}^{2}{R}_{\;}^{3}}$.分析 行星绕恒星做圆周运动万有引力提供圆周运动向心力,由此列式分析讨论即可.
解答 解:行星的轨道半径r=R+h
行星的线速度$v=\frac{2πr}{T}=\frac{2π(R+h)}{T}$
根据万有引力提供向心力:$G\frac{Mm}{(R+h)_{\;}^{2}}=m\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}(R+h)$
解得:$M=\frac{4{π}_{\;}^{2}(R+h)_{\;}^{3}}{G{T}_{\;}^{2}}$
恒星的密度为$ρ=\frac{M}{V}=\frac{\frac{4{π}_{\;}^{2}(R+h)_{\;}^{3}}{G{T}_{\;}^{2}}}{\frac{4π{R}_{\;}^{3}}{3}}=\frac{3π(R+h)_{\;}^{3}}{G{T}_{\;}^{2}{R}_{\;}^{3}}$
故答案为:$\frac{2π(R+h)}{T}$,$\frac{4{π}_{\;}^{2}(R+h)_{\;}^{3}}{G{T}_{\;}^{2}}$,$\frac{3π(R+h)_{\;}^{3}}{G{T}_{\;}^{2}{R}_{\;}^{3}}$
点评 本题根据万有引力提供圆周运动向心力展开讨论,要知道已知旋转天体的轨道半径和周期,可求得中心天体的质量.

练习册系列答案
相关题目
10. 一铁架台放于水平地面上,其上有一轻质细线悬挂一小球,开始时细线竖直,现将水平力F作用于小球上,使其缓慢地由实线位置运动到虚线位置,铁架台始终保持静止,则在这一过程中( )
一铁架台放于水平地面上,其上有一轻质细线悬挂一小球,开始时细线竖直,现将水平力F作用于小球上,使其缓慢地由实线位置运动到虚线位置,铁架台始终保持静止,则在这一过程中( )
 一铁架台放于水平地面上,其上有一轻质细线悬挂一小球,开始时细线竖直,现将水平力F作用于小球上,使其缓慢地由实线位置运动到虚线位置,铁架台始终保持静止,则在这一过程中( )
一铁架台放于水平地面上,其上有一轻质细线悬挂一小球,开始时细线竖直,现将水平力F作用于小球上,使其缓慢地由实线位置运动到虚线位置,铁架台始终保持静止,则在这一过程中( )| A. | 铁架台对地面的压力逐渐增大 | B. | 铁架台对地面的压力逐渐减小 | ||
| C. | 铁架台所受地面的摩擦力保持不变 | D. | 铁架台所受地面的摩擦力逐渐增大 |
11.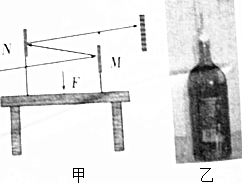 为了演示“力作用在物体上能产生微小形变”,老师做了如下两个实验:如图甲所示,在一张大桌子上放两个平面镜,让一束光依次被M和N两平面镜反射,最后射到墙上,形成一个光点,当用力压桌面时,观察墙上光点位置的变化;如图乙所示,在底部为椭圆的扁玻璃瓶中盛满红墨水,用插有细玻璃的橡皮擦封口,使水面位于细管中,当用手捏玻璃瓶时,观察细管中的水面变化.下列说法中正确的是( )
为了演示“力作用在物体上能产生微小形变”,老师做了如下两个实验:如图甲所示,在一张大桌子上放两个平面镜,让一束光依次被M和N两平面镜反射,最后射到墙上,形成一个光点,当用力压桌面时,观察墙上光点位置的变化;如图乙所示,在底部为椭圆的扁玻璃瓶中盛满红墨水,用插有细玻璃的橡皮擦封口,使水面位于细管中,当用手捏玻璃瓶时,观察细管中的水面变化.下列说法中正确的是( )
 为了演示“力作用在物体上能产生微小形变”,老师做了如下两个实验:如图甲所示,在一张大桌子上放两个平面镜,让一束光依次被M和N两平面镜反射,最后射到墙上,形成一个光点,当用力压桌面时,观察墙上光点位置的变化;如图乙所示,在底部为椭圆的扁玻璃瓶中盛满红墨水,用插有细玻璃的橡皮擦封口,使水面位于细管中,当用手捏玻璃瓶时,观察细管中的水面变化.下列说法中正确的是( )
为了演示“力作用在物体上能产生微小形变”,老师做了如下两个实验:如图甲所示,在一张大桌子上放两个平面镜,让一束光依次被M和N两平面镜反射,最后射到墙上,形成一个光点,当用力压桌面时,观察墙上光点位置的变化;如图乙所示,在底部为椭圆的扁玻璃瓶中盛满红墨水,用插有细玻璃的橡皮擦封口,使水面位于细管中,当用手捏玻璃瓶时,观察细管中的水面变化.下列说法中正确的是( )| A. | 图甲中减小对桌面的压力,墙上光点上移 | |
| B. | 图甲中增大对桌面的压力,墙上光点上移 | |
| C. | 图乙中用手沿瓶长轴方向紧捏时,管中的液面会上升 | |
| D. | 图乙中用手沿瓶短轴方向紧捏时,管中的液面会下降 |
5.关于地球同步通讯卫星,下列说法正确的是( )
| A. | 它们所在处的高度相同 | B. | 它们具有相同的质量 | ||
| C. | 它们具有相同的周期 | D. | 它们具有相同的向心力 |
9.甲、乙两质量相同的物体从同一光滑斜面的顶端下滑到底端,甲由静止开始下滑,乙以某一初速下滑,在下滑过程中( )
| A. | 甲、乙两物体动量的改变相同 | B. | 甲、乙两物体动能的改变相同 | ||
| C. | 乙的动量变化大些 | D. | 乙的动能变化大些 |
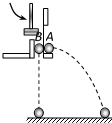 用如图所示的装置研究平抛运动,用小锤打击弹性金属片后,A球沿水平方向抛出,同时B球被松开,自由下落.A、B两球同时开始运动,多次改变打击的力度,重复这个实验,观察到两球同时落地(填“同时”或“不同时”).此实验证明平抛运动在竖直方向上的分运动是自由落体运动.(填“匀速直线运动”或“自由落体运动”)
用如图所示的装置研究平抛运动,用小锤打击弹性金属片后,A球沿水平方向抛出,同时B球被松开,自由下落.A、B两球同时开始运动,多次改变打击的力度,重复这个实验,观察到两球同时落地(填“同时”或“不同时”).此实验证明平抛运动在竖直方向上的分运动是自由落体运动.(填“匀速直线运动”或“自由落体运动”) 网球运动员沿水平方向用力击球,球离开球拍后的运动可以近似看成平抛运动,如图所示.假设网球的质量为m=0.1kg,击球时,球离地面的高度h=2.45m,获得的水平初速度大小v0=20m/s,g取10m/s2.依题意求解:
网球运动员沿水平方向用力击球,球离开球拍后的运动可以近似看成平抛运动,如图所示.假设网球的质量为m=0.1kg,击球时,球离地面的高度h=2.45m,获得的水平初速度大小v0=20m/s,g取10m/s2.依题意求解: 如图所示,在光滑水平面上有一块长为L的木板B,其上表面粗糙,在其左端有一个光滑的圆弧槽C与长木板接触但不连接,圆弧槽的下端与木板的上表面相平,B、C静止在水平面上.现有很小的滑块A以初速度v0从右端滑上B并以$\frac{{v}_{0}}{2}$的速度滑离B,恰好能到达C的最高点.A、B、C的质量均为m,试求:
如图所示,在光滑水平面上有一块长为L的木板B,其上表面粗糙,在其左端有一个光滑的圆弧槽C与长木板接触但不连接,圆弧槽的下端与木板的上表面相平,B、C静止在水平面上.现有很小的滑块A以初速度v0从右端滑上B并以$\frac{{v}_{0}}{2}$的速度滑离B,恰好能到达C的最高点.A、B、C的质量均为m,试求: