题目内容
如图所示为固定在桌面上的“C”形木块，abcd为光滑圆轨道的一部分，a为轨道的最高点，de面水平．将质量为m的小球在d点正上方h高处释放，小球自由下落到d处后沿切线进入圆形轨道运动，则（ ）
A．在h一定的条件下，释放后小球能否到a点，与小球质量有关
B．改变h的大小，就可使小球在通过a点后落回轨道之内，或者落在de面上
C．要使小球通过a点的条件是在a点的速度v>0
D．无论怎样改变h的大小，都不可能使小球在通过a点后又落回轨道内
【答案】
D
【解析】
试题分析：小球恰能通过a点的条件是小球的重力提供向心力，根据牛顿第二定律：
，要使小球能到a点，要使小球通过a点的条件是在a点速度大于等于
，根据动能定理可以求出h的最小值，与小球质量有关．故A错误，C错误，小球恰好离开a点时做平抛运动，用平抛运动的规律，水平方向的匀速直线运动：x=vt
竖直方向的自由落体运动：
，解得
，所以小球在通过a点后不可能落回轨道之内，故B错误，D正确，故选D
考点：考查功能关系、平抛运动
点评：本题难度较小，充分理解平抛运动的规律：水平方向的匀速直线运动，竖直方向的自由落体运动，它们的运动具有等时性．能根据牛顿第二定律得出小球在a点的临界速度
练习册系列答案
相关题目
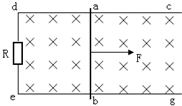如图所示，固定在水平桌面上的光滑金属杆cdeg处于方向竖直向下的匀强磁场中，金属杆ab接触良好，在端点de之间连接一电阻R，其他部分电阻不计．现用水平向右的力F作用在ab杆上，使金属杆从静止开始做匀加速运动，则能定性表示力F与时间t的关系及线框中感应电流的瞬时功率与位移X的关系的是（以向右为正方向）（ ）
如图所示，固定在水平桌面上的倾角为α=30°的光滑斜面足够长，其底端有一垂直于斜面的挡板，质量均为m的A、B两球用轻弹簧连接放在斜面上并处于静止状态，弹簧的劲度系数为k．现在将质量为3m的小球C从距离B球为s=16mg/k的地方由静止释放，C球与B球碰撞时间极短，碰撞后两球粘在一起．已知重力加速度为g，求：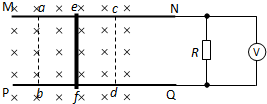
如图所示，固定在水平桌面上的光滑金属导轨MN、PQ，间距为L，其右端接有阻值为R的电阻和理想交流电压表，整个装置处在竖直向下的匀强磁场中，磁感应强度大小为B．导体棒ef垂直于导轨放置，且与两导轨接触良好，导体棒接入电路的电阻为r，其它电阻不计，现让导体棒在ab、cd之间往复运动，其速度随时间的关系为
如图所示，固定在水平桌面上的光滑金属框架cdef处于竖直向下磁感应强度为B0的匀强磁场中．金属杆ab与金属框架接触良好．此时abed构成一个边长为l的正方形，金属杆的电阻为r，其余部分电阻不计．
如图所示，固定在水平桌面上平行光滑金属导轨cd、eg之间的距离为L，d、e两点接一个阻值为R的定值电阻，整个装置处于方向竖直向下的匀强磁场中（磁场范围足够大）．有一垂直放在导轨上的金属杆ab，其质量为m、电阻值为r0在平行导轨的水平拉力F的作用下做初速度为零的匀加速直线运动，F随时间t变化规律为F=F0+kt，其中F0和k为已知的常量，经过t0时间撤去拉力F．轨道的电阻不计．求