题目内容
18. 如图所示,足够长的U形光滑金属导轨平面与水平面成θ角,与磁感应强度为B的匀强磁场垂直,导轨间距为L,上端与电阻为R连接,导轨电阻不计,ab棒的质量为m,连接电路的电阻为r,金属棒ab由静止开始沿导轨下滑,并与两导轨始终垂直且接触良好,当电阻R上产生的电热为Q时金属棒ab恰好达到最大速度,求:
如图所示,足够长的U形光滑金属导轨平面与水平面成θ角,与磁感应强度为B的匀强磁场垂直,导轨间距为L,上端与电阻为R连接,导轨电阻不计,ab棒的质量为m,连接电路的电阻为r,金属棒ab由静止开始沿导轨下滑,并与两导轨始终垂直且接触良好,当电阻R上产生的电热为Q时金属棒ab恰好达到最大速度,求:(1)金属棒ab沿导轨下滑的最大速度v
(2)金属棒ab加速运动过程中通过金属棒的电量q.
分析 (1)金属棒先做加速度减小的变加速运动,当加速度为零做匀速运动,速度达到最大.根据平衡条件和闭合电路欧姆定律结合,可求得最大速度v.
(2)通过金属棒的电量q等于平均电流与时间的乘积,根据法拉第电磁感应定律和欧姆定律结合求出平均电流,由能量守恒求得金属棒下滑的距离,联立即可得解.
解答 解:(1)金属棒达到最大速度后做匀速运动,设此时电流为I,由平衡条件有
mgsinθ=BIL
又 BLv=I(R+r)
联立得 v=$\frac{mg(R+r)sinθ}{{B}^{2}{L}^{2}}$
(2)设金属棒ab加速运动过程的位移为x,电路中的平均电流为I1,则
q=I1t
由闭合电路欧姆定律得 I1=$\frac{△Ф}{(R+r)△t}$
而磁通量的变化量△Ф=BLx
由焦耳定律得 $\frac{{Q}_{r}}{Q}$=$\frac{r}{R}$
由能量守恒定律得 mgxsinθ=(Q+Qr)+$\frac{1}{2}$mv2
解得 q=$\frac{2{B}^{4}{L}^{4}Q+{m}^{3}{g}^{2}R(R+r)si{n}^{2}θ}{2mgR{B}^{3}{L}^{3}sinθ}$
答:
(1)金属棒ab沿导轨下滑的最大速度v为$\frac{mg(R+r)sinθ}{{B}^{2}{L}^{2}}$.
(2)金属棒ab加速运动过程中通过金属棒的电量q为$\frac{2{B}^{4}{L}^{4}Q+{m}^{3}{g}^{2}R(R+r)si{n}^{2}θ}{2mgR{B}^{3}{L}^{3}sinθ}$.
点评 电磁感应综合题中,常常用到这个经验公式:感应电量q=n$\frac{△Φ}{R+r}$,常用来求位移.但在计算题中,不能直接作为公式用,要进行推导.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案 如图所示,靠皮带传动的两个轮与皮带不打滑,O1、O2分别为左、右轮的圆心,右轮半径为r,左轮半径为2r,a为左轮边缘上一点,b为右轮边缘上一点,c为左轮上一点,cO1=r,已知右轮匀速转动的角速度为ω,则( )
如图所示,靠皮带传动的两个轮与皮带不打滑,O1、O2分别为左、右轮的圆心,右轮半径为r,左轮半径为2r,a为左轮边缘上一点,b为右轮边缘上一点,c为左轮上一点,cO1=r,已知右轮匀速转动的角速度为ω,则( )| A. | 左轮角速度也为ω | |
| B. | c点的线速度大小为ωr | |
| C. | a点的线速度大小为ωr | |
| D. | a、b两点的向心加速度大小之比为2:1 |
 一个匝数为N=100的线圈在匀强磁场中匀速转动,产生的感应电动势的图象如图所示,下列说法正确的是( )
一个匝数为N=100的线圈在匀强磁场中匀速转动,产生的感应电动势的图象如图所示,下列说法正确的是( )| A. | 0.15s时刻,线圈处于与中性面相互垂直的位置 | |
| B. | 0.01s时刻,穿过线圈的磁通量为0 | |
| C. | 线圈转动的角速度为50πrad/s | |
| D. | 穿过线圈的磁通量变化率的最大值为22Wb/s |
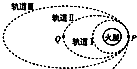 面向全球招募志愿者移民火星的“火星一号”计划,2015年2月22日公布了男女各100人的候选名单,4名华人入围.这个计划的疯狂之处在于这是一个有去无回的旅行.假设将来技术成熟,一艘飞船从火星返回地球时,经历了如图所示的变轨过程,则下列说法中正确的是( )
面向全球招募志愿者移民火星的“火星一号”计划,2015年2月22日公布了男女各100人的候选名单,4名华人入围.这个计划的疯狂之处在于这是一个有去无回的旅行.假设将来技术成熟,一艘飞船从火星返回地球时,经历了如图所示的变轨过程,则下列说法中正确的是( )| A. | 飞船在轨道Ⅱ上运动时,在P点的速度大于在Q点的速度 | |
| B. | 飞船在轨道Ⅰ上运动时的机械能大于轨道Ⅱ上运动时的机械能 | |
| C. | 飞船在轨道Ⅰ上运动到P点时的加速度小于飞船在轨道Ⅱ上运动到P点时的加速度 | |
| D. | 飞船绕火星在轨道Ⅰ上运动周期跟飞船返回地面的过程中绕地球以同样半径做圆周运动的周期相同 |
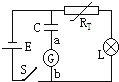 如图所示.E为电源,其内电阻不可忽略,RT为热敏电阻,其阻值随温度升高而减小,L为指示灯泡,C为平行板电容器,G为灵敏电流计.闭合开关S,当环境的温度明显升高时,下列说法正确的是( )
如图所示.E为电源,其内电阻不可忽略,RT为热敏电阻,其阻值随温度升高而减小,L为指示灯泡,C为平行板电容器,G为灵敏电流计.闭合开关S,当环境的温度明显升高时,下列说法正确的是( )| A. | 灯泡L变亮 | B. | 热敏电阻RT两端电压变大 | ||
| C. | 电容器C所带电荷量保持不变 | D. | 电流计G中电流方向由a到b |
| A. | 翟志刚需要用很大的力才能把舱盖打开是因为舱内有接近一个大气压的空气压强,而舱外的太空气压为零 | |
| B. | 翟志刚打开舱盖时,轨道舱内有与地表附近相似的空气,但由于完全失重,这些空气产生的气压为零 | |
| C. | 翟志刚打开舱盖前,轨道舱中应该已经过泄压,舱内接近真空 | |
| D. | 翟志刚打开舱盖时,轨道舱内和舱外的太空都有约为一个大气压的空气压强 |

 如图所示电路,L1和L2是两个相同的白炽灯,交流电源的电压最大值为Um,频率为f时,两灯的亮度相同,现在保持电压最大值Um不变,而频率为f增大,则L1的亮度减弱(填“增加”或“减弱”),L2的亮度增加(填“增加”或“减少”)
如图所示电路,L1和L2是两个相同的白炽灯,交流电源的电压最大值为Um,频率为f时,两灯的亮度相同,现在保持电压最大值Um不变,而频率为f增大,则L1的亮度减弱(填“增加”或“减弱”),L2的亮度增加(填“增加”或“减少”)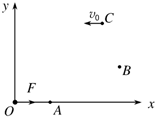 如图所示,在光滑水平面内建立直角坐标系xOy,一质点在该平面内O点受大小为F的力作用从静止开始做匀加速直线运动,经过t时间质点运动到A点,A、O两点距离为a,在A点作用力突然变为沿y轴正方向,大小仍为F,再经t时间质点运动到B点,在B点作用力又变为大小等于4F、方向始终与速度方向垂直且在该平面内的变力,再经一段时间后质点运动到C点,此时速度方向沿x轴负方向.求:
如图所示,在光滑水平面内建立直角坐标系xOy,一质点在该平面内O点受大小为F的力作用从静止开始做匀加速直线运动,经过t时间质点运动到A点,A、O两点距离为a,在A点作用力突然变为沿y轴正方向,大小仍为F,再经t时间质点运动到B点,在B点作用力又变为大小等于4F、方向始终与速度方向垂直且在该平面内的变力,再经一段时间后质点运动到C点,此时速度方向沿x轴负方向.求: