题目内容
13.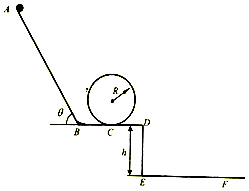 如图所示,某一在竖直平面内的轨道由倾斜轨道AB、水平轨道BC、圆轨道及水平轨道CD平滑连接而成.轨道AB与水平方向夹角θ=60°,长度L1=$\frac{9}{5}$$\sqrt{3}$m,轨道BC长度L2=$\frac{\sqrt{3}}{2}$m.D点离水平地面EF的高度h=0.9m.现将一个小球从A点由静止释放.假定轨道阻力可忽略不计,g取10m/s2.求:
如图所示,某一在竖直平面内的轨道由倾斜轨道AB、水平轨道BC、圆轨道及水平轨道CD平滑连接而成.轨道AB与水平方向夹角θ=60°,长度L1=$\frac{9}{5}$$\sqrt{3}$m,轨道BC长度L2=$\frac{\sqrt{3}}{2}$m.D点离水平地面EF的高度h=0.9m.现将一个小球从A点由静止释放.假定轨道阻力可忽略不计,g取10m/s2.求:(1)小球滑过C点时的速度大小vC;
(2)若圆轨道半径R=1m,小球在地面EF上的落点离D点的水平距离;
(3)要使小球始终不脱离圆轨道,求圆轨道半径R应满足的条件.
分析 (1)对A到C运动过程应用机械能守恒,即可求解;
(2)由机械能守恒求得在D的速度,然后根据平抛运动规律球儿水平位移;
(3)由机械能守恒求得在最高点的速度,然后应用牛顿第二定律即可.
解答 解:(1)小球运动过程只有重力做功,故机械能守恒,则有:$mg{L}_{1}sinθ=\frac{1}{2}m{{v}_{C}}^{2}$
解得:${v}_{C}=\sqrt{2g{L}_{1}sinθ}=3\sqrt{6}m/s$;
(2)设小球可通过圆轨道最高点,在圆轨道最高点速度为v,由机械能守恒可得:$mg({L}_{1}sinθ-2R)=\frac{1}{2}m{v}^{2}$
解得:$\frac{m{v}^{2}}{R}=\frac{2mg({L}_{1}sinθ-2R)}{R}=1.4mg>mg$,故小球可以通过最高点;
由机械能守恒可得:${v}_{D}={v}_{C}=3\sqrt{6}m/s$
小球从D点抛出做平抛运动,故有:$h=\frac{1}{2}g{t}^{2}$
小球在地面EF上的落点离D点的水平距离为:$x={v}_{D}t={v}_{D}\sqrt{\frac{2h}{g}}=\frac{9\sqrt{3}}{5}m$;
(3)要使小球始终不脱离圆轨道,那么在最高点的向心力不小于重力,由(2)可得:$\frac{2mg({L}_{1}sinθ-2R)}{R}≥mg$
解得:$R≤\frac{27}{25}m$;
答:(1)小球滑过C点时的速度大小vC为$3\sqrt{6}m/s$;
(2)若圆轨道半径R=1m,小球在地面EF上的落点离D点的水平距离为$\frac{9\sqrt{3}}{5}m$;
(3)要使小球始终不脱离圆轨道,圆轨道半径R应不大于$\frac{27}{25}m$.
点评 经典力学问题一般先对物体进行受力分析,求得合外力及运动过程做功情况,然后根据牛顿定律、动能定理及几何关系求解.

| A. | 电场强度为零的地方,电势一定为零 | |
| B. | 电势为零的地方,电场强度不一定为零 | |
| C. | 电场强度相同的地方,电势一定相等 | |
| D. | 电势相等的地方,电场强度一定相等 |

| A. | 大轮边缘的线速度较大 | B. | 大轮边缘的线速度较小 | ||
| C. | 两轮边缘的线速度大小相同 | D. | 大轮的角速度较大 |
| A. | mv2-mv1 | B. | 4mv2-mv1 | C. | 2(mv2-mv1) | D. | $\frac{(m{v}_{2}-m{v}_{1})}{2}$ |
| A. | 第1 s末与第3 s末的位移相同 | B. | 第1 s末与第3 s末的速度相同 | ||
| C. | 3 s末至5 s末的位移方向都相同 | D. | 3 s末至5 s末的速度方向都相同 |
| A. | 路程是1.5m | B. | 位移大小是1.5m,方向竖直向下 | ||
| C. | 位移大小是4.5m,方向竖直向下 | D. | 路程是3m |
| A. | 焦(J) | B. | 米(m) | C. | 牛(N) | D. | 秒(s) |
 如图,用跨过光滑定滑轮的缆绳将海面上一搜失去动力的小船沿直线拖向岸边.已知拖动缆绳的电动机功率恒为P=2kW,小船的质量为m=103kg,小船受到的阻力大小恒为重力的0.1倍,经过A点时的绳子的速度大小为v=1.6m/s,绳子与水平面的夹角是37?,小船从A点沿直线加速运动到B点经历时间为t1=2s,A、B两点间距离为d=2m,缆绳质量忽略不计.(sin37?=0.6,cos37?=0.8,g=10m/s2)求:
如图,用跨过光滑定滑轮的缆绳将海面上一搜失去动力的小船沿直线拖向岸边.已知拖动缆绳的电动机功率恒为P=2kW,小船的质量为m=103kg,小船受到的阻力大小恒为重力的0.1倍,经过A点时的绳子的速度大小为v=1.6m/s,绳子与水平面的夹角是37?,小船从A点沿直线加速运动到B点经历时间为t1=2s,A、B两点间距离为d=2m,缆绳质量忽略不计.(sin37?=0.6,cos37?=0.8,g=10m/s2)求: