题目内容
12. 如图所示,各个光滑斜面的顶端在同一竖直线上,底端在同一处,让各小物块(可视为质点)均从各斜面顶端由静止下滑,设斜面的倾角为θ,物块从斜面顶端下滑到底端的时间为t,下列各图象可能正确的是( )
如图所示,各个光滑斜面的顶端在同一竖直线上,底端在同一处,让各小物块(可视为质点)均从各斜面顶端由静止下滑,设斜面的倾角为θ,物块从斜面顶端下滑到底端的时间为t,下列各图象可能正确的是( )| A. |  | B. |  | C. |  | D. |  |
分析 根据牛顿第二定律求解加速度大小,根据位移时间关系推导倾角与时间的关系即可.
解答 解:设底边长度为d,则斜面长为L=$\frac{d}{cosθ}$,
根据牛顿第二定律可得加速度为:a=gsinθ,
根据位移速度关系可得:L=$\frac{1}{2}a{t}^{2}$,
解得:d=$\frac{1}{2}gsinθcosθ•{t}^{2}$=$\frac{1}{4}sin2θ•{t}^{2}$,
解得:$sin2θ=4d•\frac{1}{{t}^{2}}$,所以A正确、BCD错误;
故选:A.
点评 对于牛顿第二定律的综合应用问题,关键是弄清楚物体的运动过程和受力情况,利用牛顿第二定律或运动学的计算公式求解加速度,再根据题目要求进行解答;知道加速度是联系静力学和运动学的桥梁.

练习册系列答案
 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
3.在地面附近,存在着一个有界电场,边界MN将空间分成左右两个区域,在右区域中有水平向左的匀强电场,在右区域中离边界MN某一位置水平地面由静止释放一个质量为m的带电滑块(滑块的电荷量始终不变),如图甲所示,滑块运动的v-t图象如图乙所示,不计空气阻力,则( )


| A. | 滑块在MN右边运动的位移大小与在MN左边运动的位移大小相等 | |
| B. | 在t=5 s时,小球经过边界MN | |
| C. | 滑块受到的滑动摩擦力与电场力之比为2:5 | |
| D. | 在滑块运动的整个过程中,滑动摩擦力做的功小于电场力做的功 |
7.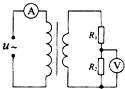 图中理想变压器的原、副线圈匝数之比为2:l,电阻R1=R2=10Ω,两电表均为理想交流电表.若R1两端电压瞬时值表达式为u1=10$\sqrt{2}$sin100πt(V),则下列说法正确的是( )
图中理想变压器的原、副线圈匝数之比为2:l,电阻R1=R2=10Ω,两电表均为理想交流电表.若R1两端电压瞬时值表达式为u1=10$\sqrt{2}$sin100πt(V),则下列说法正确的是( )
 图中理想变压器的原、副线圈匝数之比为2:l,电阻R1=R2=10Ω,两电表均为理想交流电表.若R1两端电压瞬时值表达式为u1=10$\sqrt{2}$sin100πt(V),则下列说法正确的是( )
图中理想变压器的原、副线圈匝数之比为2:l,电阻R1=R2=10Ω,两电表均为理想交流电表.若R1两端电压瞬时值表达式为u1=10$\sqrt{2}$sin100πt(V),则下列说法正确的是( )| A. | 电流表的示数为0.5A | B. | 电压表示数为14.14V | ||
| C. | R1消耗的功率为20W | D. | 原线圈输入交流电频率为100Hz |
17. 质量均为m的物块a、b之间用竖直轻弹簧相连,系在a上的细线竖直悬挂于固定点O,a、b
质量均为m的物块a、b之间用竖直轻弹簧相连,系在a上的细线竖直悬挂于固定点O,a、b
竖直粗糙墙壁接触,整个系统处于静止状态.重力加速度大小为g,则( )
 质量均为m的物块a、b之间用竖直轻弹簧相连,系在a上的细线竖直悬挂于固定点O,a、b
质量均为m的物块a、b之间用竖直轻弹簧相连,系在a上的细线竖直悬挂于固定点O,a、b 竖直粗糙墙壁接触,整个系统处于静止状态.重力加速度大小为g,则( )
| A. | 物块b可能受3个力 | B. | 细线中的拉力小于2 mg | ||
| C. | 剪断细线瞬间b的加速度大小为g | D. | 剪断细线瞬间a的加速度大小为2g |
4. 如图,两平行金属板AB长L,相距为d,当两板间加上电压U时,质量为m、带电量为q的粒子以速度V0沿两板中线进入,恰好从A极板末端离开电场.当两板间加上一个垂直于纸面的匀强磁场B时,质量为m、带电量为q的粒子同样以速度V0沿两板中线进入,恰好从B极板末端离开该区间.若同时加上U和B,质量为m、带电量为q的粒子以V0沿两板中线进入两板之间,(不计带电粒子的重力)下列说法正确的是( )
如图,两平行金属板AB长L,相距为d,当两板间加上电压U时,质量为m、带电量为q的粒子以速度V0沿两板中线进入,恰好从A极板末端离开电场.当两板间加上一个垂直于纸面的匀强磁场B时,质量为m、带电量为q的粒子同样以速度V0沿两板中线进入,恰好从B极板末端离开该区间.若同时加上U和B,质量为m、带电量为q的粒子以V0沿两板中线进入两板之间,(不计带电粒子的重力)下列说法正确的是( )
 如图,两平行金属板AB长L,相距为d,当两板间加上电压U时,质量为m、带电量为q的粒子以速度V0沿两板中线进入,恰好从A极板末端离开电场.当两板间加上一个垂直于纸面的匀强磁场B时,质量为m、带电量为q的粒子同样以速度V0沿两板中线进入,恰好从B极板末端离开该区间.若同时加上U和B,质量为m、带电量为q的粒子以V0沿两板中线进入两板之间,(不计带电粒子的重力)下列说法正确的是( )
如图,两平行金属板AB长L,相距为d,当两板间加上电压U时,质量为m、带电量为q的粒子以速度V0沿两板中线进入,恰好从A极板末端离开电场.当两板间加上一个垂直于纸面的匀强磁场B时,质量为m、带电量为q的粒子同样以速度V0沿两板中线进入,恰好从B极板末端离开该区间.若同时加上U和B,质量为m、带电量为q的粒子以V0沿两板中线进入两板之间,(不计带电粒子的重力)下列说法正确的是( )| A. | 粒子一定带正电 | B. | 粒子一定沿中线运动 | ||
| C. | 粒子一定向着A板偏离中线 | D. | 粒子一定向着B板偏离中线 |
1. 如图所示,平行金属板A、B水平正对放置,分别带等量异号电荷,一带电微粒水平射入板间,在重力和电场力共同作用下运动,轨迹如图中虚线所示,那么( )
如图所示,平行金属板A、B水平正对放置,分别带等量异号电荷,一带电微粒水平射入板间,在重力和电场力共同作用下运动,轨迹如图中虚线所示,那么( )
 如图所示,平行金属板A、B水平正对放置,分别带等量异号电荷,一带电微粒水平射入板间,在重力和电场力共同作用下运动,轨迹如图中虚线所示,那么( )
如图所示,平行金属板A、B水平正对放置,分别带等量异号电荷,一带电微粒水平射入板间,在重力和电场力共同作用下运动,轨迹如图中虚线所示,那么( )| A. | 微粒从M点运动到N点动能一定增加 | |
| B. | 微粒从M点运动到N点电势能一定增加 | |
| C. | 微粒从M点运动到N点机械能可能增加 | |
| D. | 若微粒带正电荷,则A板一定带正电荷 |
2. 如图所示的理想变压器供电的电路中,已知变压器输入电压不变,若将S闭合,则电流表A1的示数,电流表A2的示数,电流表A3的示数,电压表V的示数分别如何变化( )
如图所示的理想变压器供电的电路中,已知变压器输入电压不变,若将S闭合,则电流表A1的示数,电流表A2的示数,电流表A3的示数,电压表V的示数分别如何变化( )
 如图所示的理想变压器供电的电路中,已知变压器输入电压不变,若将S闭合,则电流表A1的示数,电流表A2的示数,电流表A3的示数,电压表V的示数分别如何变化( )
如图所示的理想变压器供电的电路中,已知变压器输入电压不变,若将S闭合,则电流表A1的示数,电流表A2的示数,电流表A3的示数,电压表V的示数分别如何变化( )| A. | 变小 变大 变小 不变 | B. | 变大 变小 变大 不变 | ||
| C. | 不变 变大 变大 不变 | D. | 不变 变大 变大 变小 |
 在如图所示的竖直平面内,一个直角三角形金属线框顶点C与MN重合,在水平线MN的下方有足够大的匀强磁场,线框由静止释放,沿轴线BC方向竖直落入磁场中.忽略空气阻力,从释放到线框完全进入磁场过程中,关于线框运动的v-t图,可能正确的是( )
在如图所示的竖直平面内,一个直角三角形金属线框顶点C与MN重合,在水平线MN的下方有足够大的匀强磁场,线框由静止释放,沿轴线BC方向竖直落入磁场中.忽略空气阻力,从释放到线框完全进入磁场过程中,关于线框运动的v-t图,可能正确的是( )



 考驾驶证的某环节,学员需要将车前轮停在指定的感应线上.如图所示,车在感应线前以v0的速度匀速行驶,前轮到感应线的距离为s时,学员立即刹车,假设刹车后,车受到的阻力为其总重力(包括车内的人)的μ倍.已知车(包括车内的人)的质量为M,讨论车的初速度v0不同的情况停下时,车前轮相对感应线的位置.
考驾驶证的某环节,学员需要将车前轮停在指定的感应线上.如图所示,车在感应线前以v0的速度匀速行驶,前轮到感应线的距离为s时,学员立即刹车,假设刹车后,车受到的阻力为其总重力(包括车内的人)的μ倍.已知车(包括车内的人)的质量为M,讨论车的初速度v0不同的情况停下时,车前轮相对感应线的位置.