题目内容
1. 有三本同样的书叠放在水平桌面上,如图所示,假如每本书重G=5N,它们之间及书与桌面间的动摩擦因数均为μ=0.4,如果水平抽出第一本或第二本或第三本书,至少要用多大拉力?请通过计算来说明各种情况.
有三本同样的书叠放在水平桌面上,如图所示,假如每本书重G=5N,它们之间及书与桌面间的动摩擦因数均为μ=0.4,如果水平抽出第一本或第二本或第三本书,至少要用多大拉力?请通过计算来说明各种情况.
分析 水平抽出第一本拉力至少等于第一本书所受的最大静摩擦力.当第一本书与第二本书间、第二本书与第三本书间的静摩擦力都达到最大时,第二本书刚好被抽出,此时,第三本书静止不动,以上面两本书为研究对象,根据牛顿第二定律求解.以三本书整体为研究对象,求出水平抽出第三本书所用的最小拉力.
解答 解:要水平抽出第一本,拉力至少等于第一本书所受的最大静摩擦力,为 F1=μG=0.4×5N=2N
当第一本书与第二本书间、第二本书与第三本书间的静摩擦力都达到最大时,第二本书刚好被抽出.
以第一本书为研究对象,由牛顿第二定律得 μG=ma1,
以上面两本书为研究对象,根据牛顿第二定律得 F2-μ•2G=2ma1,
联立解得 F2=8N
当第二本书与第三本书间、第三本书与桌面间的静摩擦力都达到最大时,第三本书刚好被抽出.
以上面两本书为研究对象,根据牛顿第二定律得 μ•2G=2ma2,
以三本书整体为研究对象,根据牛顿第二定律得 F3-μ•3G=3ma2,联立解得
联立解得 F3=12N
答:水平抽出第一本或第二本或第三本书,分别至少要用2N、8N和12N的拉力.
点评 本题要注意当静摩擦力达到最大静摩擦力时,是两者将发生相对滑动的临界状态,结合整体法和隔离法进行研究.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
11. 如图所示,MN和PQ是电阻不计的光滑平行金属导轨,间距为L,导轨弯曲部分与平直部分平滑连接,顶端弯曲部分与平直部分平滑连接,顶端接一个阻值为R的定值电阻,平直导轨左端,平直导轨左端,有宽度为d,方向竖直向上,磁感应强度大小为B的匀强磁场,一电阻为r,长为L的金属棒从导轨AA′处由静止释放,经过磁场右边界后继续向右运动并从桌边水平飞出,已知AA′离桌面高度为h,桌面离地高度为H,金属棒落地点的水平位移为s,重力加速度为g,由此可求出金属棒穿过磁场区域的过程中( )
如图所示,MN和PQ是电阻不计的光滑平行金属导轨,间距为L,导轨弯曲部分与平直部分平滑连接,顶端弯曲部分与平直部分平滑连接,顶端接一个阻值为R的定值电阻,平直导轨左端,平直导轨左端,有宽度为d,方向竖直向上,磁感应强度大小为B的匀强磁场,一电阻为r,长为L的金属棒从导轨AA′处由静止释放,经过磁场右边界后继续向右运动并从桌边水平飞出,已知AA′离桌面高度为h,桌面离地高度为H,金属棒落地点的水平位移为s,重力加速度为g,由此可求出金属棒穿过磁场区域的过程中( )
 如图所示,MN和PQ是电阻不计的光滑平行金属导轨,间距为L,导轨弯曲部分与平直部分平滑连接,顶端弯曲部分与平直部分平滑连接,顶端接一个阻值为R的定值电阻,平直导轨左端,平直导轨左端,有宽度为d,方向竖直向上,磁感应强度大小为B的匀强磁场,一电阻为r,长为L的金属棒从导轨AA′处由静止释放,经过磁场右边界后继续向右运动并从桌边水平飞出,已知AA′离桌面高度为h,桌面离地高度为H,金属棒落地点的水平位移为s,重力加速度为g,由此可求出金属棒穿过磁场区域的过程中( )
如图所示,MN和PQ是电阻不计的光滑平行金属导轨,间距为L,导轨弯曲部分与平直部分平滑连接,顶端弯曲部分与平直部分平滑连接,顶端接一个阻值为R的定值电阻,平直导轨左端,平直导轨左端,有宽度为d,方向竖直向上,磁感应强度大小为B的匀强磁场,一电阻为r,长为L的金属棒从导轨AA′处由静止释放,经过磁场右边界后继续向右运动并从桌边水平飞出,已知AA′离桌面高度为h,桌面离地高度为H,金属棒落地点的水平位移为s,重力加速度为g,由此可求出金属棒穿过磁场区域的过程中( )| A. | 流过金属棒的最小电流 | B. | 通过金属棒的电荷量 | ||
| C. | 金属棒克服安培力所做的功 | D. | 金属棒产生的焦耳热 |
9. 如图所示,在磁感应强度B=1.0T的匀强磁场中,金属杆PQ在外力F作用下在粗糙U形导轨上以速度v=2m/s向右匀速滑动,两导轨间距离l=1.0m,电阻R=3.0Ω,金属杆的电阻r=1.0Ω,导轨电阻忽略不计,则下列说法正确的是( )
如图所示,在磁感应强度B=1.0T的匀强磁场中,金属杆PQ在外力F作用下在粗糙U形导轨上以速度v=2m/s向右匀速滑动,两导轨间距离l=1.0m,电阻R=3.0Ω,金属杆的电阻r=1.0Ω,导轨电阻忽略不计,则下列说法正确的是( )
 如图所示,在磁感应强度B=1.0T的匀强磁场中,金属杆PQ在外力F作用下在粗糙U形导轨上以速度v=2m/s向右匀速滑动,两导轨间距离l=1.0m,电阻R=3.0Ω,金属杆的电阻r=1.0Ω,导轨电阻忽略不计,则下列说法正确的是( )
如图所示,在磁感应强度B=1.0T的匀强磁场中,金属杆PQ在外力F作用下在粗糙U形导轨上以速度v=2m/s向右匀速滑动,两导轨间距离l=1.0m,电阻R=3.0Ω,金属杆的电阻r=1.0Ω,导轨电阻忽略不计,则下列说法正确的是( )| A. | 通过R的感应电流的方向为由a到d | |
| B. | 金属杆PQ切割磁感线产生的感应电动势的大小为2.0 V | |
| C. | 金属杆PQ受到的安培力大小为0.5 N | |
| D. | 外力F做功的数值等于电路产生的焦耳热 |
6. 如图,质量为m1的滑块A置于水平地面上,质量为m2的滑块B在一水平力作用下紧靠滑块A(A、B接触面竖直),此时A恰好不滑动,B刚好不下滑.A与B间的动摩擦因数为μ1,A与地面问的动摩擦因数为μ2,重力加速度为g,最大静摩擦力等于滑动摩擦力.下列说法正确的是( )
如图,质量为m1的滑块A置于水平地面上,质量为m2的滑块B在一水平力作用下紧靠滑块A(A、B接触面竖直),此时A恰好不滑动,B刚好不下滑.A与B间的动摩擦因数为μ1,A与地面问的动摩擦因数为μ2,重力加速度为g,最大静摩擦力等于滑动摩擦力.下列说法正确的是( )
 如图,质量为m1的滑块A置于水平地面上,质量为m2的滑块B在一水平力作用下紧靠滑块A(A、B接触面竖直),此时A恰好不滑动,B刚好不下滑.A与B间的动摩擦因数为μ1,A与地面问的动摩擦因数为μ2,重力加速度为g,最大静摩擦力等于滑动摩擦力.下列说法正确的是( )
如图,质量为m1的滑块A置于水平地面上,质量为m2的滑块B在一水平力作用下紧靠滑块A(A、B接触面竖直),此时A恰好不滑动,B刚好不下滑.A与B间的动摩擦因数为μ1,A与地面问的动摩擦因数为μ2,重力加速度为g,最大静摩擦力等于滑动摩擦力.下列说法正确的是( )| A. | A与B间的摩擦力大小为μ1m2g | B. | A与B间的摩擦力大小为μ2m2g | ||
| C. | A与地面间的摩擦力大小为μ1m1g | D. | $\frac{{m}_{1}}{{m}_{2}}$=$\frac{1-{μ}_{1}{μ}_{2}}{{μ}_{1}{μ}_{2}}$ |
13.悬崖跳水是一项极具挑战性的极限运动,需要运动员具有非凡的胆量和过硬的技术.跳水运动员进入水中后受到水的阻力而做减速运动,设质量为m的运动员刚入水时的速度为v,水对他的阻力大小恒为F,那么在他减速下降深度为h的过程中,下列说法正确的是(g为当地的重力加速度)( )
| A. | 他的动能减少了(F-mg)h | B. | 他的重力势能减小了$mgh-\frac{1}{2}m{v^2}$ | ||
| C. | 他的机械能减少了Fh | D. | 他的机械能减少了mgh |
 如图所示,正方形闭合导线框的质量可以忽略不计,将它从如图所示的位置匀速拉出匀强磁场.若第一次用0.3s时间拉出,外力所做的功为W1;第二次用0.9s时间拉出,外力所做的功为W2,则W1:W2=3:1.
如图所示,正方形闭合导线框的质量可以忽略不计,将它从如图所示的位置匀速拉出匀强磁场.若第一次用0.3s时间拉出,外力所做的功为W1;第二次用0.9s时间拉出,外力所做的功为W2,则W1:W2=3:1.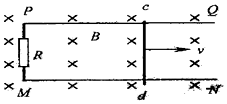 空间某区域存在水平方向的匀强磁场,磁感应强度B=1.0T,在磁场区域内有两根相距L=0.8m的平行金属导轨PQ、MN,固定在竖直平面内,如图所示,PM间连接有R=3.0Ω的电阻,导体棒cd沿导轨平面向右匀速运动,在回路中产生的电流I=0.6A,求:
空间某区域存在水平方向的匀强磁场,磁感应强度B=1.0T,在磁场区域内有两根相距L=0.8m的平行金属导轨PQ、MN,固定在竖直平面内,如图所示,PM间连接有R=3.0Ω的电阻,导体棒cd沿导轨平面向右匀速运动,在回路中产生的电流I=0.6A,求: