题目内容
19.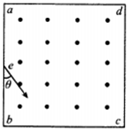 如图所示空间存在着边长为L的正方形磁场区域abcd,其磁场方向垂直于纸面向外且磁感应强度大小为B,一电荷量为-q的点电荷由ab中点e点与ab夹θ=37°入射,速度大小未知,重力作用忽略不计且忽略磁场边界效应,则下列说法正确的是( )
如图所示空间存在着边长为L的正方形磁场区域abcd,其磁场方向垂直于纸面向外且磁感应强度大小为B,一电荷量为-q的点电荷由ab中点e点与ab夹θ=37°入射,速度大小未知,重力作用忽略不计且忽略磁场边界效应,则下列说法正确的是( )| A. | 不同大小的速度入射,则在磁场区域运动的时间有可能相同 | |
| B. | 伴随点电荷速度的增加其在磁场区域运动的时间逐渐减小 | |
| C. | 伴随点电荷速度大小的增加,其离开磁场点可能在ea、ad段任意一点 | |
| D. | 伴随点电荷速度大小的增加,其在bc山的出射点距点c的长度为0.625L |
分析 如果速度较小,则粒子从ea边射出时轨迹对应的圆心角相等,由此分析射出时间大小;画出粒子运动轨迹,利用几何关系求解分析粒子射出点的位置,并计算射出点的距离即可.
解答 解:A、如果速度较小,则粒子从ea边射出时轨迹对应的圆心角相等,根据$t=\frac{θ}{2π}T$可知运动的时间相等,A正确;
B、如果速度较小,则粒子从ea边射出时轨迹对应的圆心角相等,粒子在磁场中运动的时间不变,B错误;
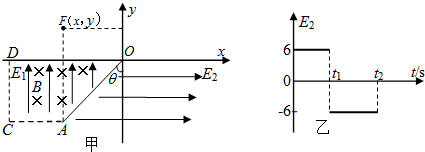
C、点电荷速度大小的增加,其离开磁场点在ea、ad段的临界轨迹如图所示,
所以其离开磁场点在ea、ad段有一段距离不会出现,C错误;
D、粒子速度增大时刚好与bc边相切时轨迹如图所示,
根据几何关系可得Rsin37°=R-$\frac{L}{2}$,解得R=1.25L,所以x=Rcos37°=L;
即粒子轨迹与bc边的切点为c点;
粒子速度增大时从bc边射出,射出点到b点的最近距离为$\frac{L}{2}tan37°=0.375L$,所以粒子在bc边上的出射点距点c的长度为L-0.375L=0.625L,D正确.
故选:AD.
点评 对于带电粒子在磁场中的运动情况分析,一般是确定圆心位置,根据几何关系求半径,结合洛伦兹力提供向心力求解未知量;根据周期公式结合轨迹对应的圆心角求时间.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.如图为一物体作直线运动的速度时间图象,下列说法正确的是( )


| A. | 物体在第2s初的速度为6m/s | |
| B. | 物体在3~5s内静止 | |
| C. | 物体在0~2s内做加速运动 | |
| D. | 物体在前2s内的加速度大于最后1s内的加速度值 |
5.飞机的起飞过程是从静止出发,在直跑道上加速前进,等达到一定速度时离地.已知飞机加速前进的路程为1600m,所用的时间为40s,假设这段时间内的运动为匀加速运动,则飞机离地时的速度为( )
| A. | 50m/s | B. | 60m/s | C. | 70m/s | D. | 80m/s |
14. 如图所示,质量为m的木块A放在斜面体B上,A和B接触面间动摩擦因数为μ,若A和B沿水平方向保持相对静止以加速一起向右做匀加速直线运动,则AB间的摩擦力大小为( )
如图所示,质量为m的木块A放在斜面体B上,A和B接触面间动摩擦因数为μ,若A和B沿水平方向保持相对静止以加速一起向右做匀加速直线运动,则AB间的摩擦力大小为( )
 如图所示,质量为m的木块A放在斜面体B上,A和B接触面间动摩擦因数为μ,若A和B沿水平方向保持相对静止以加速一起向右做匀加速直线运动,则AB间的摩擦力大小为( )
如图所示,质量为m的木块A放在斜面体B上,A和B接触面间动摩擦因数为μ,若A和B沿水平方向保持相对静止以加速一起向右做匀加速直线运动,则AB间的摩擦力大小为( )| A. | ma | B. | mgsinθ | C. | μmgcosθ | D. | mgsinθ+macosθ |

 如图所示,将小物体(可视为质点)置于水平桌面上的长木板上,用水平细线通过轻质定滑轮用钩码牵引长木板.若长木板的质量m1=1.0kg,小物体的质量m2=0.5kg,小物体与长木板左边缘的距离d=0.09m,已知各接触面间的动摩擦因数均为μ=0.2,最大静摩擦力等于滑动摩擦力,重力加速度g=10m/s2.
如图所示,将小物体(可视为质点)置于水平桌面上的长木板上,用水平细线通过轻质定滑轮用钩码牵引长木板.若长木板的质量m1=1.0kg,小物体的质量m2=0.5kg,小物体与长木板左边缘的距离d=0.09m,已知各接触面间的动摩擦因数均为μ=0.2,最大静摩擦力等于滑动摩擦力,重力加速度g=10m/s2.