题目内容
3. 教室里有同学利用磁性黑板玩游戏,现将游戏简化如图所示,黑板高为H,可视为质点的小磁铁质量为m,以速度v竖直向上抛出,小磁铁与黑板正对时,受到的吸引力可近似为恒力F,方向指向黑板,抛出点与黑板下沿等高且水平距离为L,若磁铁在上升过程中恰好被吸在黑板的上沿(设磁铁碰到黑板即被吸住,不考虑反弹),F、H、m及重力加速度g为已知量,问:
教室里有同学利用磁性黑板玩游戏,现将游戏简化如图所示,黑板高为H,可视为质点的小磁铁质量为m,以速度v竖直向上抛出,小磁铁与黑板正对时,受到的吸引力可近似为恒力F,方向指向黑板,抛出点与黑板下沿等高且水平距离为L,若磁铁在上升过程中恰好被吸在黑板的上沿(设磁铁碰到黑板即被吸住,不考虑反弹),F、H、m及重力加速度g为已知量,问:(1)请写出抛出速度v与水平距离L的关系式;
(2)L取多大时有最小的抛出速度v0,最小的速度v0为多少?
分析 小磁铁在竖直方向做竖直上抛运动,在水平方向做匀加速直线运动;由运动的合成与分解规律可明确初速度与L的关系;再由数学规律可求得最小速度.
解答 解:(1)小球水平方向的加速度a=$\frac{F}{m}$;
由运动学公式可得:L=$\frac{1}{2}$at2=$\frac{1}{2}$$\frac{F}{m}{t}^{2}$
解得:t=$\sqrt{\frac{2mL}{F}}$;
竖直方向做减速运动,加速度为-g;
则有:
H=v0t-$\frac{1}{2}$gt2=v0$\sqrt{\frac{2mL}{F}}$-$\frac{1}{2}$g($\sqrt{\frac{2mL}{F}}$)2;
解得v0=$\frac{2H+g(\sqrt{\frac{2mL}{F}})^{2}}{\sqrt{\frac{2mL}{F}}}$=$\frac{2H}{\sqrt{\frac{2mL}{F}}}$+g$\sqrt{\frac{2mL}{F}}$
(2)由数学规律均值不等式可得:
当$\frac{2H}{\sqrt{\frac{2mL}{F}}}$=g$\sqrt{\frac{2mL}{F}}$时速度取最小值;
即当L=$\frac{FH}{mg}$时,v0最小,最小值为:2$\sqrt{2gH}$
答:(1)出速度v与水平距离L的关系式为v0=$\frac{2H}{\sqrt{\frac{2mL}{F}}}$+g$\sqrt{\frac{2mL}{F}}$
(2)L取$\frac{FH}{mg}$时,v0最小;最小的速度v0为2$\sqrt{2gH}$
点评 本题考查运动的合成与分解的应用,难点在于函数关系的正确应用,要掌握应用数学规律解决物理问题的方法.

练习册系列答案
相关题目
13. 绝缘水平面上固定一正点电荷Q,另一质量为m、电荷量为-q(q>0)的滑块(可看作点电荷)从a点以初速度v0沿水平面向Q运动,到达b点时速度减为零.已知a、b间距离为s,滑块与水平面间的动摩擦因数为μ,重力加速度为g.以下判断正确的是( )
绝缘水平面上固定一正点电荷Q,另一质量为m、电荷量为-q(q>0)的滑块(可看作点电荷)从a点以初速度v0沿水平面向Q运动,到达b点时速度减为零.已知a、b间距离为s,滑块与水平面间的动摩擦因数为μ,重力加速度为g.以下判断正确的是( )
 绝缘水平面上固定一正点电荷Q,另一质量为m、电荷量为-q(q>0)的滑块(可看作点电荷)从a点以初速度v0沿水平面向Q运动,到达b点时速度减为零.已知a、b间距离为s,滑块与水平面间的动摩擦因数为μ,重力加速度为g.以下判断正确的是( )
绝缘水平面上固定一正点电荷Q,另一质量为m、电荷量为-q(q>0)的滑块(可看作点电荷)从a点以初速度v0沿水平面向Q运动,到达b点时速度减为零.已知a、b间距离为s,滑块与水平面间的动摩擦因数为μ,重力加速度为g.以下判断正确的是( )| A. | 此过程中产生的内能大于$\frac{m{v}_{0}^{2}}{2}$ | |
| B. | 滑块在运动过程的中间时刻,速度的大小等于$\frac{{v}_{0}}{2}$ | |
| C. | 滑块在运动过程中所受Q的库仑力有可能大于滑动摩擦力 | |
| D. | Q产生的电场中,a、b两点间电势差的大小为${U_{ab}}=\frac{m(v_0^2-μgs)}{2q}$ |
14. 飞镖比赛是一项极具观赏性的体育比赛项目,2010年的IDF(国际飞镖联合会)飞镖世界杯赛在上海进行.某一选手在距地面高h,离靶面的水平距离L处,将质量为m的飞镖以速度v0水平投出,结果飞镖落在靶心正上方.如只改变h、L、m、v0四个量中的一个,可使飞镖投中靶心的是(不计空气阻力)( )
飞镖比赛是一项极具观赏性的体育比赛项目,2010年的IDF(国际飞镖联合会)飞镖世界杯赛在上海进行.某一选手在距地面高h,离靶面的水平距离L处,将质量为m的飞镖以速度v0水平投出,结果飞镖落在靶心正上方.如只改变h、L、m、v0四个量中的一个,可使飞镖投中靶心的是(不计空气阻力)( )
 飞镖比赛是一项极具观赏性的体育比赛项目,2010年的IDF(国际飞镖联合会)飞镖世界杯赛在上海进行.某一选手在距地面高h,离靶面的水平距离L处,将质量为m的飞镖以速度v0水平投出,结果飞镖落在靶心正上方.如只改变h、L、m、v0四个量中的一个,可使飞镖投中靶心的是(不计空气阻力)( )
飞镖比赛是一项极具观赏性的体育比赛项目,2010年的IDF(国际飞镖联合会)飞镖世界杯赛在上海进行.某一选手在距地面高h,离靶面的水平距离L处,将质量为m的飞镖以速度v0水平投出,结果飞镖落在靶心正上方.如只改变h、L、m、v0四个量中的一个,可使飞镖投中靶心的是(不计空气阻力)( )| A. | 适当减小v0 | B. | 适当提高h | C. | 适当减小m | D. | 适当增加L |
15.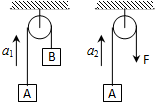 如图所示,一细绳跨过一轻质定滑轮(不计细绳和滑轮质量,不计滑轮与轴之间摩擦),绳的一端悬挂一质量为m的物体A,另一端悬挂一质量为M(M>m)的物体B,此时A物体的加速度为a1,如果用力F代替物体B,使物体A产生的加速度为a2,那么( )
如图所示,一细绳跨过一轻质定滑轮(不计细绳和滑轮质量,不计滑轮与轴之间摩擦),绳的一端悬挂一质量为m的物体A,另一端悬挂一质量为M(M>m)的物体B,此时A物体的加速度为a1,如果用力F代替物体B,使物体A产生的加速度为a2,那么( )
 如图所示,一细绳跨过一轻质定滑轮(不计细绳和滑轮质量,不计滑轮与轴之间摩擦),绳的一端悬挂一质量为m的物体A,另一端悬挂一质量为M(M>m)的物体B,此时A物体的加速度为a1,如果用力F代替物体B,使物体A产生的加速度为a2,那么( )
如图所示,一细绳跨过一轻质定滑轮(不计细绳和滑轮质量,不计滑轮与轴之间摩擦),绳的一端悬挂一质量为m的物体A,另一端悬挂一质量为M(M>m)的物体B,此时A物体的加速度为a1,如果用力F代替物体B,使物体A产生的加速度为a2,那么( )| A. | 如果a1=a2,则F<Mg | B. | 如果F=Mg,则a1<a2 | ||
| C. | 如果a1=a2,则F=Mg | D. | 如果F=$\frac{2mMg}{m+M}$,则a1=a2 |
13. 如图所示,整个空间存在水平向左的匀强电场,一长为L的绝缘轻质细硬杆一端固定在O点,另一端固定一个质量为m、电荷量为+q的小球P,杆可绕O点在竖直平面内无摩擦转动,电场的电场强度大小为E=$\frac{\sqrt{3}mg}{3q}$,先把杆拉成水平,然后将杆无初速度释放、重力加速度为g,不计空气阻力,则( )
如图所示,整个空间存在水平向左的匀强电场,一长为L的绝缘轻质细硬杆一端固定在O点,另一端固定一个质量为m、电荷量为+q的小球P,杆可绕O点在竖直平面内无摩擦转动,电场的电场强度大小为E=$\frac{\sqrt{3}mg}{3q}$,先把杆拉成水平,然后将杆无初速度释放、重力加速度为g,不计空气阻力,则( )
 如图所示,整个空间存在水平向左的匀强电场,一长为L的绝缘轻质细硬杆一端固定在O点,另一端固定一个质量为m、电荷量为+q的小球P,杆可绕O点在竖直平面内无摩擦转动,电场的电场强度大小为E=$\frac{\sqrt{3}mg}{3q}$,先把杆拉成水平,然后将杆无初速度释放、重力加速度为g,不计空气阻力,则( )
如图所示,整个空间存在水平向左的匀强电场,一长为L的绝缘轻质细硬杆一端固定在O点,另一端固定一个质量为m、电荷量为+q的小球P,杆可绕O点在竖直平面内无摩擦转动,电场的电场强度大小为E=$\frac{\sqrt{3}mg}{3q}$,先把杆拉成水平,然后将杆无初速度释放、重力加速度为g,不计空气阻力,则( )| A. | 小球到最低点时速度最大 | |
| B. | 小球从开始至最低点过程中动能先增大后减小 | |
| C. | 小球对杆的最大拉力大小为$\frac{8\sqrt{3}}{3}$mg | |
| D. | 小球可绕O点做完整的圆周运动 |
 在匀强磁场中(磁感应强度为B)有一折导线abc,ab=bc=L,θ=60°,导线中的电流方向如图所示,电流强度为I,求该折导线受到安培力的大小和方向.
在匀强磁场中(磁感应强度为B)有一折导线abc,ab=bc=L,θ=60°,导线中的电流方向如图所示,电流强度为I,求该折导线受到安培力的大小和方向.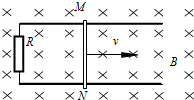 如图所示,宽度为L=0.2m的足够长的平行光滑金属导轨固定在绝缘水平面上,导轨的一端连接阻值为R=1.0Ω的电阻.导轨所在空间存在竖直向下的匀强磁场,磁感应强度大小为B=0.2T.一根质量为m=10g的导体棒MN放在导轨上,并与导轨始终接触良好,导轨和导体棒的电阻均可忽略不计.现用垂直MN的水平拉力F拉动导体棒沿导轨向右匀速运动,速度为v=5.0m/s,在运动过程中保持导体棒与导轨垂直.求:
如图所示,宽度为L=0.2m的足够长的平行光滑金属导轨固定在绝缘水平面上,导轨的一端连接阻值为R=1.0Ω的电阻.导轨所在空间存在竖直向下的匀强磁场,磁感应强度大小为B=0.2T.一根质量为m=10g的导体棒MN放在导轨上,并与导轨始终接触良好,导轨和导体棒的电阻均可忽略不计.现用垂直MN的水平拉力F拉动导体棒沿导轨向右匀速运动,速度为v=5.0m/s,在运动过程中保持导体棒与导轨垂直.求: