题目内容
3. 如图所示,水平面上质量相等的两木块A、B用一轻弹簧相连,整个系统处于静止状态.t=0时刻起用一竖直向上的力F拉动木块A,使A向上做匀加速直线运动.t1时刻弹簧恰好恢复原长,t2时刻木块B恰好要离开水平面.以下说法正确的是( )
如图所示,水平面上质量相等的两木块A、B用一轻弹簧相连,整个系统处于静止状态.t=0时刻起用一竖直向上的力F拉动木块A,使A向上做匀加速直线运动.t1时刻弹簧恰好恢复原长,t2时刻木块B恰好要离开水平面.以下说法正确的是( )| A. | 在0-t2时间内,拉力F随时间t均匀增加 | |
| B. | 在0-t2时间内,拉力F随木块A的位移均匀增加 | |
| C. | 在0-t1时间内,拉力F做的功等于A的动能增量 | |
| D. | 在0-t2时间内,拉力F做的功等于A的机械能增量 |
分析 以木块A为研究对象,分析受力情况,根据牛顿第二定律得出F与A位移x的关系式,再根据位移时间公式,得出F与t的关系.根据功能关系分析拉力做功与A的机械能增量关系.
解答 解:A、B、设原来系统静止时弹簧的压缩长度为x0,当木块A的位移为x时,弹簧的压缩长度为(x0-x),弹簧的弹力大小为k(x0-x),根据牛顿第二定律得:
F+k(x0-x)-mg=ma
得到:F=kx-kx0+ma+mg,
又kx0=mg,
则得到:F=kx+ma
可见F与x是线性关系,则在0-t2时间内,拉力F随木块A的位移均匀增加,由x=$\frac{1}{2}$at2得:F=k$\frac{1}{2}$at2+ma,F与t不成正比.故A错误,B正确.
C、根据动能定理可知:在0-t1时间内,拉力F做的功、重力做功与弹力做功之和等于A的动能增量,故C错误.
D、据题t=0时刻弹簧的弹力等于A的重力,t2时刻弹簧的弹力等于B的重力,而两个物体的重力相等,所以t=0时刻和t2时刻弹簧的弹力相等,弹性势能相等,根据功能关系可知在0-t2间间内,拉力F做的功等于A的机械能增量,故D正确.
故选:BD.
点评 对于匀变速直线运动,运用根据牛顿第二定律研究力的大小是常用的思路.分析功能关系时,要注意分析隐含的相等关系,要抓住t=0时刻和t2时刻弹簧的弹性势能相等进行研究.

练习册系列答案
相关题目
13. 有一种电荷控制式喷墨打印机的打印头的结构简图如图所示.其中墨盒可以喷出极小的墨汁微粒,此微粒经过带电室后以一定的初速度垂直射入偏转电场,再经偏转电场后打到纸上,显示出字符.现为了使打在纸上的字迹缩小,下列措施可行的是( )
有一种电荷控制式喷墨打印机的打印头的结构简图如图所示.其中墨盒可以喷出极小的墨汁微粒,此微粒经过带电室后以一定的初速度垂直射入偏转电场,再经偏转电场后打到纸上,显示出字符.现为了使打在纸上的字迹缩小,下列措施可行的是( )
 有一种电荷控制式喷墨打印机的打印头的结构简图如图所示.其中墨盒可以喷出极小的墨汁微粒,此微粒经过带电室后以一定的初速度垂直射入偏转电场,再经偏转电场后打到纸上,显示出字符.现为了使打在纸上的字迹缩小,下列措施可行的是( )
有一种电荷控制式喷墨打印机的打印头的结构简图如图所示.其中墨盒可以喷出极小的墨汁微粒,此微粒经过带电室后以一定的初速度垂直射入偏转电场,再经偏转电场后打到纸上,显示出字符.现为了使打在纸上的字迹缩小,下列措施可行的是( )| A. | 减小墨汁微粒所带的电荷量 | B. | 减小墨汁微粒的质量 | ||
| C. | 增大墨汁微粒的喷出速度 | D. | 增大偏转板间的电压 |
8.下列关于布朗运动的说法,正确的是( )
| A. | 液体温度越高,布朗运动越剧烈 | |
| B. | 悬浮粒子越大,布朗运动越剧烈 | |
| C. | 布朗运动是由于液体各部分的温度不同而引起的 | |
| D. | 布朗运动就是液体分子的无规则运动 |
15.一带电荷量为+q、质量为m的带电粒子从O点以速率v0射入电场,运动到A点时速率为2v0.现有另一电荷量为-2q、质量为m的粒子仍以速率v0从O点射入该电场,运动到B点时速率为2v0.若忽略重力的影响,带电粒子从O到A和从O到B的运动过程中( )
| A. | 在O、A、B三点中,B点电势最高 | |
| B. | 在O、A、B三点中,A点电势最高 | |
| C. | 带电荷量为+q的粒子电势能的变化量大 | |
| D. | 两粒子的电势能变化量相等 |
12. 如图,小车上有固定支架,支架上用细线拴一个小球,线长为l(小球可看作质点),小车与球一起以速度v0沿水平向左匀速运动,当小车突然碰到矮墙后,车立即停止运动,此后小球升高的最大高度不可能是(线未拉断)( )
如图,小车上有固定支架,支架上用细线拴一个小球,线长为l(小球可看作质点),小车与球一起以速度v0沿水平向左匀速运动,当小车突然碰到矮墙后,车立即停止运动,此后小球升高的最大高度不可能是(线未拉断)( )
 如图,小车上有固定支架,支架上用细线拴一个小球,线长为l(小球可看作质点),小车与球一起以速度v0沿水平向左匀速运动,当小车突然碰到矮墙后,车立即停止运动,此后小球升高的最大高度不可能是(线未拉断)( )
如图,小车上有固定支架,支架上用细线拴一个小球,线长为l(小球可看作质点),小车与球一起以速度v0沿水平向左匀速运动,当小车突然碰到矮墙后,车立即停止运动,此后小球升高的最大高度不可能是(线未拉断)( )| A. | 等于$\frac{{{v}_{0}}^{2}}{2g}$ | B. | 小于$\frac{{{v}_{0}}^{2}}{2g}$ | C. | 大于$\frac{{{v}_{0}}^{2}}{2g}$ | D. | 等于2l |
13.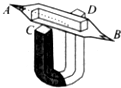 如图所示是用阴极射线管演示电子在磁场中受洛伦兹力的实验装置,图中虚线是电子的运动轨迹,那么下列关于此装置的说法正确的是( )
如图所示是用阴极射线管演示电子在磁场中受洛伦兹力的实验装置,图中虚线是电子的运动轨迹,那么下列关于此装置的说法正确的是( )
 如图所示是用阴极射线管演示电子在磁场中受洛伦兹力的实验装置,图中虚线是电子的运动轨迹,那么下列关于此装置的说法正确的是( )
如图所示是用阴极射线管演示电子在磁场中受洛伦兹力的实验装置,图中虚线是电子的运动轨迹,那么下列关于此装置的说法正确的是( )| A. | A端接的是高压直流电源的正极 | B. | C端是蹄形磁铁的N极 | ||
| C. | C端是蹄形磁铁的S极 | D. | 以上说法均不对 |

 如图所示,一宽为40cm的匀强磁场区域,磁场方向垂直纸面向里,一边长为20cm的正方形导线框位于纸面内,以垂直于磁场边界、垂直磁场的恒定速度v=20cm/s通过磁场区域,在运动过程中,线框有一边始终与磁场区域的边界平行,取线框刚进入磁场的时刻t=0,在下图所示的图象中,正确反映线框中感应电流随时间变化规律的是(以逆时针方向为正)( )
如图所示,一宽为40cm的匀强磁场区域,磁场方向垂直纸面向里,一边长为20cm的正方形导线框位于纸面内,以垂直于磁场边界、垂直磁场的恒定速度v=20cm/s通过磁场区域,在运动过程中,线框有一边始终与磁场区域的边界平行,取线框刚进入磁场的时刻t=0,在下图所示的图象中,正确反映线框中感应电流随时间变化规律的是(以逆时针方向为正)( )



 有平行边界的匀强磁场,方向垂直纸面向里,宽度为d,一带电粒子质量为m,电荷量为q,以垂直于左边界,垂直磁场的初速度v0进入磁场,从右边界穿出时速度方向相对进入时的方向偏角为θ,不计粒子重力,求:
有平行边界的匀强磁场,方向垂直纸面向里,宽度为d,一带电粒子质量为m,电荷量为q,以垂直于左边界,垂直磁场的初速度v0进入磁场,从右边界穿出时速度方向相对进入时的方向偏角为θ,不计粒子重力,求: