题目内容
15. 如图所示,A,B,C,D为四个完全相同的光滑圆柱体,质量均为m,两块相同的光滑竖直挡板在大小相等的水平推力F作用下使四个圆柱体处于静止状态,如图所示已知当地的重力加速度为g,则有( )
如图所示,A,B,C,D为四个完全相同的光滑圆柱体,质量均为m,两块相同的光滑竖直挡板在大小相等的水平推力F作用下使四个圆柱体处于静止状态,如图所示已知当地的重力加速度为g,则有( )| A. | 力F的最小值为$\sqrt{3}$mg | B. | 力F的最大值为$\sqrt{3}$mg | ||
| C. | B球对A球的弹力大小等于mg | D. | 若减小F,则B和A之间的弹力增加 |
分析 当A球与B球之间的弹力等于零时,F最小,对B球受力分析,根据几何关系求出F的最小值,根据分析可知,B球对A球的弹力大小不是恒定的值,可以为零.
解答 解:A、当A球与B球之间的弹力等于零时,F最小,对B球受力分析,如图所示:
根据几何关系可知,θ=30°,
则$tan30°=\frac{mg}{F}$,解得:F=$\sqrt{3}mg$,所以F的最小值为$\sqrt{3}mg$,故A正确,B错误;
C、B球对A球的弹力大小可以等于零,故C错误;
D、当F$>\sqrt{3}mg$时,A对B有弹力作用,若减小F,则B和A之间的弹力减小,当F=$\sqrt{3}mg$时,AB之间的弹力建为零,故D错误.
故选:A
点评 本题主要考查了共点力平衡的直接应用,知道当A球与B球之间的弹力等于零时F最小,并能根据几何关系求出角度与力的大小,难度适中.

练习册系列答案
相关题目
5. 由天津去上海,可以乘火车,也可以乘轮船,如图,曲线ACB和虚线ADB分别表示天津到上海的铁路线和海上路线,线段AB表示天津到上海的直线距离,则下列说法中正确的是( )
由天津去上海,可以乘火车,也可以乘轮船,如图,曲线ACB和虚线ADB分别表示天津到上海的铁路线和海上路线,线段AB表示天津到上海的直线距离,则下列说法中正确的是( )
 由天津去上海,可以乘火车,也可以乘轮船,如图,曲线ACB和虚线ADB分别表示天津到上海的铁路线和海上路线,线段AB表示天津到上海的直线距离,则下列说法中正确的是( )
由天津去上海,可以乘火车,也可以乘轮船,如图,曲线ACB和虚线ADB分别表示天津到上海的铁路线和海上路线,线段AB表示天津到上海的直线距离,则下列说法中正确的是( )| A. | 乘火车通过的路程等于位移的大小 | B. | 乘轮船通过的路程等于位移的大小 | ||
| C. | 乘火车与轮船通过的位移相等 | D. | 乘火车与轮船通过的路程一定相等 |
6. 如图所示,木块A静止在斜面体B上.设木块受到斜面体的支持力大小为N,摩擦力大小为f.当斜面体水平向左做加速度逐渐增大的加速运动时,若木块A相对于斜面体B始终保持
如图所示,木块A静止在斜面体B上.设木块受到斜面体的支持力大小为N,摩擦力大小为f.当斜面体水平向左做加速度逐渐增大的加速运动时,若木块A相对于斜面体B始终保持
静止,则( )
 如图所示,木块A静止在斜面体B上.设木块受到斜面体的支持力大小为N,摩擦力大小为f.当斜面体水平向左做加速度逐渐增大的加速运动时,若木块A相对于斜面体B始终保持
如图所示,木块A静止在斜面体B上.设木块受到斜面体的支持力大小为N,摩擦力大小为f.当斜面体水平向左做加速度逐渐增大的加速运动时,若木块A相对于斜面体B始终保持静止,则( )
| A. | N增大,f增大 | B. | N不变,f增大 | ||
| C. | N减小,f先增大后减小 | D. | N增大,f先减小后增大 |
3.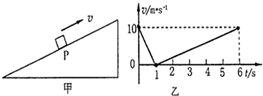 如图甲所示,质量m=1kg的物块(可视为质点)以v0=10m/s的初速度从粗糙斜面上的P点沿斜面向上运动到达最高点后,又沿原路返回,其速率随时间变化的图象如图乙所示,已知斜面固定且足够长.且不计空气阻力,取g=10m/s2.下列说法中正确的是( )
如图甲所示,质量m=1kg的物块(可视为质点)以v0=10m/s的初速度从粗糙斜面上的P点沿斜面向上运动到达最高点后,又沿原路返回,其速率随时间变化的图象如图乙所示,已知斜面固定且足够长.且不计空气阻力,取g=10m/s2.下列说法中正确的是( )
 如图甲所示,质量m=1kg的物块(可视为质点)以v0=10m/s的初速度从粗糙斜面上的P点沿斜面向上运动到达最高点后,又沿原路返回,其速率随时间变化的图象如图乙所示,已知斜面固定且足够长.且不计空气阻力,取g=10m/s2.下列说法中正确的是( )
如图甲所示,质量m=1kg的物块(可视为质点)以v0=10m/s的初速度从粗糙斜面上的P点沿斜面向上运动到达最高点后,又沿原路返回,其速率随时间变化的图象如图乙所示,已知斜面固定且足够长.且不计空气阻力,取g=10m/s2.下列说法中正确的是( )| A. | 物块所受的重力与摩擦力之比为3:2 | |
| B. | 在t=1s到t=6s的时间内物块所受重力的平均功率为50W | |
| C. | 在t=0到t=1s时间内机械能的变化量大小与t=1s到t=6s时间内机械能变化量大小之比为1:5 | |
| D. | 在t=6s时物体克服摩擦力做功的功率为20W |
20.下列说法正确的是( )
| A. | 竖直平面内做匀速圆周运动的物体,其合外力可能不指向圆心 | |
| B. | 匀速直线运动和自由落体运动的合运动一定是曲线运动 | |
| C. | 做曲线运动的物体的加速度可能是不变的 | |
| D. | 火车超过限定速度转弯时,车轮轮缘可能挤压铁轨的内轨 |
5.关于元电荷,下述正确的是( )
| A. | 点电荷就是元电荷 | B. | 元电荷就是正电子 | ||
| C. | 元电荷是带电量为1C的电荷 | D. | 自然界中已知的最小电荷量 |
 如图所示,公路上有一辆公共汽车以10m/s的速度匀速行驶,为了平稳停靠在站台,在距离站台P左侧位置60m处开始刹车做匀减速直线运动.同时一个人为了搭车,从距站台P右侧位置40m处从静止正对着站台跑去,假设人先做匀加速直线运动,速度达到4m/s后匀速运动一段时间,接着做匀减速直线运动,最终人和车到达P位置同时停下,人加速和减速时的加速度大小相等.求:
如图所示,公路上有一辆公共汽车以10m/s的速度匀速行驶,为了平稳停靠在站台,在距离站台P左侧位置60m处开始刹车做匀减速直线运动.同时一个人为了搭车,从距站台P右侧位置40m处从静止正对着站台跑去,假设人先做匀加速直线运动,速度达到4m/s后匀速运动一段时间,接着做匀减速直线运动,最终人和车到达P位置同时停下,人加速和减速时的加速度大小相等.求: