题目内容
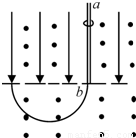 如图所示,虚线上方有方向竖直向下的匀强电场,虚线上下有相同的匀强磁场,磁感应强度为B,方向垂直纸面向外,ab是一根长为l的绝缘细杆,沿电场线放置在虚线上方,b端恰在虚线上,将一套在杆上的带电量为q、质量为m的小环(小环重力忽略不计),从a端由静止释放后,小环先作加速运动,后作匀速运动到达b端,已知小环与绝缘杆间的动摩擦系数为μ,当小环脱离杆进入虚线下方后,运动轨迹是半圆,圆的半径是
如图所示,虚线上方有方向竖直向下的匀强电场,虚线上下有相同的匀强磁场,磁感应强度为B,方向垂直纸面向外,ab是一根长为l的绝缘细杆,沿电场线放置在虚线上方,b端恰在虚线上,将一套在杆上的带电量为q、质量为m的小环(小环重力忽略不计),从a端由静止释放后,小环先作加速运动,后作匀速运动到达b端,已知小环与绝缘杆间的动摩擦系数为μ,当小环脱离杆进入虚线下方后,运动轨迹是半圆,圆的半径是 ,求:
,求:(1)小环到达b点的速度vb;
(2)匀强电场的场强E.
【答案】分析:通过洛伦兹力提供向心力,并结合半径长度,从而求出小环到达b点的速度;
根据小环受力平衡方程,可知匀强电场强度.
解答:解:
(1)小环在磁场中做匀速圆周运动,由洛仑兹力提供向心力:
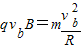
又因R=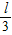
解得b点速度为: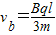
(2)小环在沿杆向下运动时,受力情况如图所示:
当小环在杆上做匀速运动时由平衡条件得
在水平方向有:N=qvbB (1)
在竖直方向有:qE=f (2)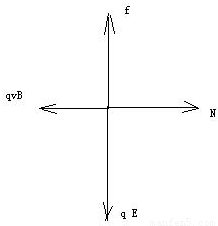
又因摩擦力:f=μN (3)
由(1)(2)(3)式解得,匀强电场的场强E为: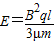
答:(1)小环到达b点的速度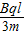 ;
;
(2)匀强电场的场强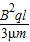 .
.
点评:考查牛顿第二定律、受力平衡方程,洛伦兹力与电场力公式,本题属于基础的.
根据小环受力平衡方程,可知匀强电场强度.
解答:解:
(1)小环在磁场中做匀速圆周运动,由洛仑兹力提供向心力:
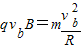
又因R=
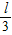
解得b点速度为:
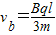
(2)小环在沿杆向下运动时,受力情况如图所示:
当小环在杆上做匀速运动时由平衡条件得
在水平方向有:N=qvbB (1)
在竖直方向有:qE=f (2)

又因摩擦力:f=μN (3)
由(1)(2)(3)式解得,匀强电场的场强E为:
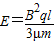
答:(1)小环到达b点的速度
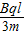 ;
;(2)匀强电场的场强
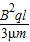 .
.点评:考查牛顿第二定律、受力平衡方程,洛伦兹力与电场力公式,本题属于基础的.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 (2009?中山市模拟)如图所示,虚线上方有场强为E的匀强电场,方向竖直向下,虚线上下有磁感应强度相同的匀强磁场,方向垂直纸面向外,ab是一根长为l的绝缘细杆,沿电场线放置在虚线上方的场中,b端在虚线上,将一套在杆上的带正电的小球从a端由静止释放后,小球先作加速运动,后作匀速运动到达b端,已知小球与绝缘杆间的动摩擦系数μ=0.3,小球重力忽略不计,当小球脱离杆进入虚线下方后,运动轨迹是半圆,圆的半径是
(2009?中山市模拟)如图所示,虚线上方有场强为E的匀强电场,方向竖直向下,虚线上下有磁感应强度相同的匀强磁场,方向垂直纸面向外,ab是一根长为l的绝缘细杆,沿电场线放置在虚线上方的场中,b端在虚线上,将一套在杆上的带正电的小球从a端由静止释放后,小球先作加速运动,后作匀速运动到达b端,已知小球与绝缘杆间的动摩擦系数μ=0.3,小球重力忽略不计,当小球脱离杆进入虚线下方后,运动轨迹是半圆,圆的半径是 如图所示,虚线上方有场强为E的匀强电场,方向竖直向下,虚线上下有磁感应强度相同的匀强磁场,大小为B,方向垂直纸面向外,ab是一根长为L的绝缘细杆,沿电场线放置在虚线上方的场中,b端在虚线上.将一套在杆上的带正电的轻小球,带电量为q,质量为m,从a端由静止释放,小球到达b端前已做匀速运动.已知小球与绝缘杆间的动摩擦因数为μ,小球重力忽略不计,当小球脱离杆进入虚线下方的磁场,求:
如图所示,虚线上方有场强为E的匀强电场,方向竖直向下,虚线上下有磁感应强度相同的匀强磁场,大小为B,方向垂直纸面向外,ab是一根长为L的绝缘细杆,沿电场线放置在虚线上方的场中,b端在虚线上.将一套在杆上的带正电的轻小球,带电量为q,质量为m,从a端由静止释放,小球到达b端前已做匀速运动.已知小球与绝缘杆间的动摩擦因数为μ,小球重力忽略不计,当小球脱离杆进入虚线下方的磁场,求: