题目内容
1.一列队伍长120m,正以某一速度匀速直线运动,因为紧急情况需通知排头兵,一通讯员以不变的速率跑步从队尾赶到排头又从排头返回队尾,在此过程中队伍前进了288m,求通讯员在此过程中通过的路程和位移各多大?分析 设通讯员的速度为v1,队伍的速度为v2,通讯员从队尾到队头的时间为t1,从队头到队尾的时间为t2,队伍前进用时间为t.以队伍为参照物,可求通讯员从队尾往队头的速度,从队头往队尾的速度,利用速度公式求通讯员从队尾到队头的时间t1,通讯员从队头到队尾的时间为t2,队伍前进288用的时间t,而t=t1+t2,据此列方程求出v1、v2的关系,进而求出在t时间内通讯员行走的路程,位移即为队伍前进的位移.
解答 解:设通讯员的速度为v1,队伍的速度为v2,通讯员从队尾到队头的时间为t1,从队头到队尾的时间为t2,队伍前进用时间为t.
由通讯员往返总时间与队伍运动时间相等可得如下方程:
t=t1+t2,
即:$\frac{288}{{v}_{2}}=\frac{120}{{v}_{1}-{v}_{2}}+\frac{120}{{v}_{1}+{v}_{2}}$
整理上式得:6v12-5v1v2-6v22=0
解上式得:v1=$\frac{3}{2}$v2
将上式等号两边同乘总时间t,
即v1t=$\frac{3}{2}$v2t
v1t即为通讯员走过的路程s1,v2t即为队伍前进距离s2,则有
s1=$\frac{3}{2}$s2=432m,
排头兵从队尾出发又回到队尾,则运动得位移即为队伍前进的位移,即x=288m.
答:通讯员在此过程中通过的路程为432m,位移为288m.
点评 本题考查路程的计算,关键是计算向前的距离和向后的距离,难点是知道向前的时候人和队伍前进方向相同,向后的时候人和队伍前进方向相反,解决此类问题常常用到相对运动的知识.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
2.以下说法正确的是( )
| A. | 布朗运动是液体分子无规则的运动 | |
| B. | 食盐晶体的物理性质沿各个方向都是一样的 | |
| C. | 气体的温度变化时,其分子平均动能和分子间势能也随之改变 | |
| D. | 用活塞压缩气缸里的空气,对空气做功2.0×105J,若空气向外界放出热量1.5×105J,则空气内能增加5×104J | |
| E. | 清晨草叶上的露珠是由空气中的水汽凝结成的水珠,这一物理过程中,水分子间的引力、斥力都增大 |
3.下列说法正确的是( )
| A. | 氡的半衰期为3.8天,若取8个氡原子核,经7.6天后就一定剩下2个原子核了 | |
| B. | 原子核内的中子转化成一个质子和一个电子,这种转化产生的电子发射到核外,就是β粒子,这就是β衰变的实质 | |
| C. | 光子的能量由光的频率所决定 | |
| D. | 只要有核反应发生,就一定会释放出核能 | |
| E. | 按照玻尔理论,氢原子核外电子从半径较小的轨道跃迁到半径较大的轨道时,电子的动能减小,电势能增大,原子的总能量增加 |
13.如图是测定两个电源的电动势和内电阻实验中得到的U-I图线,则应有( )
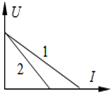

| A. | 当I1=I2时,电源总功率P1=P2 | |
| B. | 当I1=I2时,外电阻R1>R2 | |
| C. | 当U1=U2时,电源输出功率P出1<P出2 | |
| D. | 当U1=U2时,电源内部消耗的电功率P内1>P内2 |
10.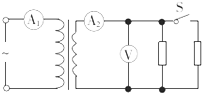 图示是一理想变压器的电路连接图,变压器原线圈两端加有正弦交变电压,副线圈接有两个定值电阻,当开关S闭合到断开时,各理想电表示数的变化是( )
图示是一理想变压器的电路连接图,变压器原线圈两端加有正弦交变电压,副线圈接有两个定值电阻,当开关S闭合到断开时,各理想电表示数的变化是( )
 图示是一理想变压器的电路连接图,变压器原线圈两端加有正弦交变电压,副线圈接有两个定值电阻,当开关S闭合到断开时,各理想电表示数的变化是( )
图示是一理想变压器的电路连接图,变压器原线圈两端加有正弦交变电压,副线圈接有两个定值电阻,当开关S闭合到断开时,各理想电表示数的变化是( )| A. | 电流表 、 、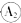 的示数变小,电压表 的示数变小,电压表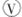 的示数变大 的示数变大 | |
| B. | 电流表 、 、 的示数变小,电压表 的示数变小,电压表 的示数不变 的示数不变 | |
| C. | 电流表 、 、 的示数变小,电压表 的示数变小,电压表 的示数变小 的示数变小 | |
| D. | 电流表 、 、 的示数变大,电压表 的示数变大,电压表 的示数变大 的示数变大 |
 2015年亚洲极限滑板邀请赛在合肥之心城购物中心外广场火热上演,顶尖高手齐聚霸都带来极限盛宴.如图所示,滑板轨道BC为竖直平面内的四分之一圆弧赛道,半径为R=1.8m,ABC为光滑轨道,且水平轨道AB与圆弧BC在B点相切.若运动员的质量M=48.0kg,滑板质量m=2.0kg,二者均可视为质点,重力加速度g取值10m/s2,不计空气阻力求:
2015年亚洲极限滑板邀请赛在合肥之心城购物中心外广场火热上演,顶尖高手齐聚霸都带来极限盛宴.如图所示,滑板轨道BC为竖直平面内的四分之一圆弧赛道,半径为R=1.8m,ABC为光滑轨道,且水平轨道AB与圆弧BC在B点相切.若运动员的质量M=48.0kg,滑板质量m=2.0kg,二者均可视为质点,重力加速度g取值10m/s2,不计空气阻力求:
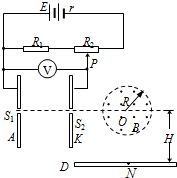 如图所示为一个自动控制装置的工作原理简图.在电路中,电源电动势E=91V,内阻r=1.0Ω,定值电阻R1=10Ω,滑动变阻器R2的最大阻值为80Ω.在以O为圆心,半径为R=10$\sqrt{3}$cm的圆形区域内,有一个方向垂直纸面向外的水平匀强磁场,磁感应强度大小为B=0.10T.竖直平行放置的两金属板A、K相距为d,S1、S2为A、K板上的两个小孔,且S1、S2跟O在竖直极板的同一直线上,OS2=2R,另有一水平放置的足够长的荧光屏D,O点跟荧光屏D点之间的距离为H.比荷为2.0×105C/kg的离子流由S1进入电场后,通过S2向磁场中心射去,通过磁场后落到荧光屏D上.离子进入电场的初速度、重力、离子之间的作用力均可忽略不计.问:
如图所示为一个自动控制装置的工作原理简图.在电路中,电源电动势E=91V,内阻r=1.0Ω,定值电阻R1=10Ω,滑动变阻器R2的最大阻值为80Ω.在以O为圆心,半径为R=10$\sqrt{3}$cm的圆形区域内,有一个方向垂直纸面向外的水平匀强磁场,磁感应强度大小为B=0.10T.竖直平行放置的两金属板A、K相距为d,S1、S2为A、K板上的两个小孔,且S1、S2跟O在竖直极板的同一直线上,OS2=2R,另有一水平放置的足够长的荧光屏D,O点跟荧光屏D点之间的距离为H.比荷为2.0×105C/kg的离子流由S1进入电场后,通过S2向磁场中心射去,通过磁场后落到荧光屏D上.离子进入电场的初速度、重力、离子之间的作用力均可忽略不计.问: