题目内容
5.人造卫星沿圆形轨道绕地球运行,由于大气阻力作用使其高度逐渐降低,则它的( )| A. | 角速度减小 | B. | 线速度增大 | C. | 周期减小 | D. | 向心加速度减小 |
分析 根据万有引力提供向心力得出线速度、角速度、向心加速度、周期与轨道半径的关系,从而进行比较.
解答 解:人造卫星绕地球做匀速圆周运动,根据万有引力提供向心力,设卫星的质量为m、轨道半径为r、地球质量为M,有
$G\frac{Mm}{{r}^{2}}=m\frac{{v}^{2}}{r}=m{ω}^{2}r=m\frac{4{π}^{2}r}{{T}^{2}}=ma$
A、角速度ω=$\sqrt{\frac{GM}{{r}^{3}}}$,知轨道半径减小,角速度增大,故A错误;
B、线速度v=$\sqrt{\frac{GM}{r}}$,知轨道半径减小,线速度增大,故B正确;
C、周期T=2$π\sqrt{\frac{{r}^{3}}{GM}}$,知轨道半径减小,周期减小,故C正确;
D、向心加速度a=$\frac{GM}{{r}^{2}}$,知轨道半径减小,向心加速度增大,故D错误;
故选:BC
点评 解决本题的关键掌握万有引力提供向心力列出等式,会根据轨道半径的变化,判断线速度、角速度、周期、向心加速度的变化.

练习册系列答案
相关题目
20.如图所示,有关地球人造卫星轨道的正确说法有( )


| A. | a、b、c均可能是卫星轨道 | B. | 卫星轨道只可能是a | ||
| C. | a、b均可能是卫星轨道 | D. | b可能是同步卫星的轨道 |
14.一轻杆一端固定质量为m的小球,以另一端为圆心在竖直平面内作圆周运动,轻杆长为l,以下说法中正确的是( )
| A. | 小球过最高点时,杆的弹力可以等于零 | |
| B. | 小球过最高点时的最小速度为$\sqrt{gl}$ | |
| C. | 小球到最高点时速度v>0,小球一定能通过最高点做圆周运动 | |
| D. | 小球过最高点时,杆对球的作用力一定与小球所受重力方向相反 |
11.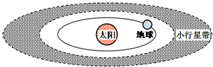 如图所示,在地球轨道外侧有一小行星带.假设行星带中的小行星都只受到太阳的引力,并绕太阳做匀速圆周运动.下列说法正确的是( )
如图所示,在地球轨道外侧有一小行星带.假设行星带中的小行星都只受到太阳的引力,并绕太阳做匀速圆周运动.下列说法正确的是( )
 如图所示,在地球轨道外侧有一小行星带.假设行星带中的小行星都只受到太阳的引力,并绕太阳做匀速圆周运动.下列说法正确的是( )
如图所示,在地球轨道外侧有一小行星带.假设行星带中的小行星都只受到太阳的引力,并绕太阳做匀速圆周运动.下列说法正确的是( )| A. | 各小行星绕太阳运动的周期小于一年 | |
| B. | 小行星带内各行星绕太阳公转的线速度均小于地球公转的线速度 | |
| C. | 小行星带内侧行星的加速度小于外侧行星的加速度 | |
| D. | 与太阳距离相等的每一颗小行星,受到太阳的引力大小都相等 |
 已知弹簧的弹性势能的表达式为Ep=$\frac{1}{2}$kx2,其中k为弹簧的劲度系数,x为弹簧的形变量,现有一轻质弹簧竖直放置在水平面上,如图,今将一质量为m的物块轻放在弹簧上,试求当物块下落到最低点时的加速度.
已知弹簧的弹性势能的表达式为Ep=$\frac{1}{2}$kx2,其中k为弹簧的劲度系数,x为弹簧的形变量,现有一轻质弹簧竖直放置在水平面上,如图,今将一质量为m的物块轻放在弹簧上,试求当物块下落到最低点时的加速度. 在“研究平抛物体的运动”的实验中:
在“研究平抛物体的运动”的实验中: 用油膜法估测分子的大小,方法及实验步骤如下:
用油膜法估测分子的大小,方法及实验步骤如下: