题目内容
6.选取无限远处电势为0,均匀带电球表面的电势大小可表示为φ=$\frac{Q}{4π?R}$(其中Q为电量的绝对值,R为球的半径,ε为介电常数),某球形电容器由半径分别为RA、RB的同心金属球壳构成,请根据电容器的定义式计算该球形电容器的电容为( )| A. | C=4π?$\frac{{R}_{A}+{R}_{B}}{\sqrt{{R}_{A}{R}_{B}}}$ | B. | C=4π?$\frac{{R}_{B}-{R}_{A}}{\sqrt{{R}_{A}{R}_{B}}}$ | C. | C=4π?$\frac{{R}_{B}{R}_{A}}{{R}_{B}-{R}_{A}}$ | D. | C=4π?$\frac{{R}_{B}{R}_{A}}{{R}_{B}+{R}_{A}}$ |
分析 根据球面的电动势的表达式,求得两球壳间的电势,即可求得电势差,根据C=$\frac{Q}{U}$求得电容器的电容
解答 解:设RA>RB,RA带负电荷,RB上带正电荷,则B上的电势为:$φ=\frac{Q}{4π?{R}_{B}}$,A上的电势为:${φ}_{A}=\frac{-Q}{4π?{R}_{A}}$,故BA间的电势差为:U=φ-φA
电容器的电容为:C=$\frac{Q}{U}$
联立解得:C=4π?$\frac{{R}_{B}{R}_{A}}{{R}_{B}+{R}_{A}}$
故选:D
点评 本题主要考查了电容器的定义式,关键是抓住带正负电的球壳具有的电势,即可根据C=$\frac{Q}{U}$求得电容大小

练习册系列答案
相关题目
8. 如图所示,由两种单色光混合而成的一复色光线射向一块半圆柱形玻璃砖圆心O,经折射后分别沿oa和ob射出玻璃砖.下列说法正确的是( )
如图所示,由两种单色光混合而成的一复色光线射向一块半圆柱形玻璃砖圆心O,经折射后分别沿oa和ob射出玻璃砖.下列说法正确的是( )
 如图所示,由两种单色光混合而成的一复色光线射向一块半圆柱形玻璃砖圆心O,经折射后分别沿oa和ob射出玻璃砖.下列说法正确的是( )
如图所示,由两种单色光混合而成的一复色光线射向一块半圆柱形玻璃砖圆心O,经折射后分别沿oa和ob射出玻璃砖.下列说法正确的是( )| A. | 玻璃砖对a光的折射率小于对b光的折射率 | |
| B. | 在玻璃中,a光的传播速度大于b光的传播速度 | |
| C. | 在真空中,a光的传播速度小于b光的传播速度 | |
| D. | 若改变光束的入射方向使θ角逐渐变大,则折射光线a首先消失 |
18. 如图重物G压在纸带上.用水平力F慢慢拉动纸带,重物跟着一起运动,若迅速拉动纸带,纸带会从重物下抽出,下列说法正确的是( )
如图重物G压在纸带上.用水平力F慢慢拉动纸带,重物跟着一起运动,若迅速拉动纸带,纸带会从重物下抽出,下列说法正确的是( )
 如图重物G压在纸带上.用水平力F慢慢拉动纸带,重物跟着一起运动,若迅速拉动纸带,纸带会从重物下抽出,下列说法正确的是( )
如图重物G压在纸带上.用水平力F慢慢拉动纸带,重物跟着一起运动,若迅速拉动纸带,纸带会从重物下抽出,下列说法正确的是( )| A. | 慢拉时,重物和纸带间的摩擦力大 | B. | 快拉时,重物和纸带间的摩擦力大 | ||
| C. | 慢拉时,纸带给重物的冲量大 | D. | 快拉时,纸带给重物的冲量大 |
16.下列几种运动,物体机械能守恒的是( )
| A. | 小球做平抛运动 | B. | 火车进站停靠 | ||
| C. | 雨滴匀速直线下落 | D. | 滑块沿光滑固定斜面自由下滑 |
 如图所示,足够长的直线ab靠近通电螺线管的一端,且与螺线管垂直.用磁传感器测量ab上各点沿ab方向上的磁感应强度分量Bx的大小,在计算机屏幕上显示的图象大致是( )
如图所示,足够长的直线ab靠近通电螺线管的一端,且与螺线管垂直.用磁传感器测量ab上各点沿ab方向上的磁感应强度分量Bx的大小,在计算机屏幕上显示的图象大致是( )







 如图所示,是某同学探究“机械能守恒定律”的实验装置图.在水平桌面上固定一个斜面,斜面上固定一个气垫导轨,导轨的顶端A处有一个附有长方形遮光片的小滑块,遮光片的宽度为b,小滑块连同遮光片的总质量为M,左端由跨过光滑轻质定滑轮的细绳与一个质量为m,(Mgsinθ>mg)的小球相连;小球距地面的距离为H,遮光片的两条长边与导轨斜面AC垂直;导轨上距离A点为x的B点处有一个光电门.现将小滑块从A点由静止释放,测量出遮光片经过光电门的时间为t,导轨与水平桌面间的夹角为θ,重力加速度为g.则:
如图所示,是某同学探究“机械能守恒定律”的实验装置图.在水平桌面上固定一个斜面,斜面上固定一个气垫导轨,导轨的顶端A处有一个附有长方形遮光片的小滑块,遮光片的宽度为b,小滑块连同遮光片的总质量为M,左端由跨过光滑轻质定滑轮的细绳与一个质量为m,(Mgsinθ>mg)的小球相连;小球距地面的距离为H,遮光片的两条长边与导轨斜面AC垂直;导轨上距离A点为x的B点处有一个光电门.现将小滑块从A点由静止释放,测量出遮光片经过光电门的时间为t,导轨与水平桌面间的夹角为θ,重力加速度为g.则: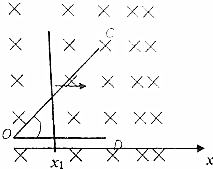 如图.水平面内有一“∠”型光滑金属导轨COD,电阻不计,∠COD=45°.足够长直导体棒搁在导轨上,单位长度的电阻为r=0.5Ω,导体棒垂直OD.空间存在垂直于导轨平面的磁场,以O点为原点沿0D方向建立坐标轴,导轨间x>0一侧存在沿x方向均匀增大的稳恒磁场,变化率为0.5T/m,O点磁感应强度B0=1T.在外力作用下,棒以一定的初速度向右做直线运动,运动时回路中的电流强度保持不变.已知运动到图中x1=1m位置时,速度大小v1=2m/s,则回路中的电流强度大小为6A,从x1=1m位置再向右运动1m的过程中,通过导体棒的电量为3.5C.
如图.水平面内有一“∠”型光滑金属导轨COD,电阻不计,∠COD=45°.足够长直导体棒搁在导轨上,单位长度的电阻为r=0.5Ω,导体棒垂直OD.空间存在垂直于导轨平面的磁场,以O点为原点沿0D方向建立坐标轴,导轨间x>0一侧存在沿x方向均匀增大的稳恒磁场,变化率为0.5T/m,O点磁感应强度B0=1T.在外力作用下,棒以一定的初速度向右做直线运动,运动时回路中的电流强度保持不变.已知运动到图中x1=1m位置时,速度大小v1=2m/s,则回路中的电流强度大小为6A,从x1=1m位置再向右运动1m的过程中,通过导体棒的电量为3.5C.