题目内容
16. 如图,河宽L=60m,一只小船在河的正中央航行,经过O点时发现在距船S=40m的下游有一瀑布,为了使小船在A点安全靠岸,在O点立即调整好船头的指向,不至被冲进瀑布中.若河水的流速大小恒为5m/s,则小船的最小航行速率为3m/s.若河水的流速与到河岸的最短距离x成正比,即v水=kx(x≤$\frac{L}{2}$,k为一常量),小船在O点调整船头垂直河岸,让小船保持航行速率不变到达A点,则小船在平行河岸方向做匀减速运动.
如图,河宽L=60m,一只小船在河的正中央航行,经过O点时发现在距船S=40m的下游有一瀑布,为了使小船在A点安全靠岸,在O点立即调整好船头的指向,不至被冲进瀑布中.若河水的流速大小恒为5m/s,则小船的最小航行速率为3m/s.若河水的流速与到河岸的最短距离x成正比,即v水=kx(x≤$\frac{L}{2}$,k为一常量),小船在O点调整船头垂直河岸,让小船保持航行速率不变到达A点,则小船在平行河岸方向做匀减速运动.
分析 小船离河岸30m处,要使能安全到达河岸,则小船的合运动最大位移为$\sqrt{3{0}^{2}+4{0}^{2}}$m=50m.因此由水流速度与小船的合速度,借助于平行四边形定则,即可求出小船在静水中最小速度;并依据v水=kx=kv船t,即可判定水流方向的运动性质.
解答 解:要使小船避开危险区沿直线到达对岸,则有合运动的最大位移为OA=$\sqrt{3{0}^{2}+4{0}^{2}}$m=50m.
根据题目中的图,那个30m 和40m 要构成一个直角三角形的两条边,那么斜边就是50m了,那么正弦就是$\frac{3}{5}$,
这是一个路程的三角形,再找一个速度的三角形,就是船速和水流速为直角边的,水流速是5m/s,而且这两个是相似三角形,
所以那个正弦乘以5m/s就行了,5×$\frac{3}{5}$=3m/s,
因此船的速度最小速率为3m/s,
若河水的流速与到河岸的最短距离x成正比,小船在O点调整船头垂直河岸,让小船保持航行速率不变到达A点,
v水=kx=kv船t,则小船在平行河岸方向速度在均匀减小,则做匀减速直线运动,
故答案为:3,匀减速.
点评 本题属于:一个速度要分解,已知一个分速度的大小与方向,还已知另一个分速度的大小且最小,则求这个分速度的方向与大小值.这种题型运用平行四边形定则,由几何关系来确定最小值.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
7.物理学家通过艰辛的实验和理论研究探究自然规律,为人类的科学做出了巨大贡献,值得我们敬仰.下列描述中符合物理学史实的是( )
| A. | 奥斯特根据通电螺线管的磁场和条形磁铁的磁场相似性,提出了分子电流假说 | |
| B. | 开普勒发现了行星运动三定律,进而提出了万有引力定律 | |
| C. | 平均速度、瞬时速度和加速度等描述运动所需要的概念是伽利略首先建立的 | |
| D. | 法拉第发现了电磁感应现象并总结出了判断感应电流方向的规律 |
4.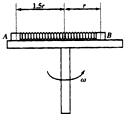 如图所示,水平转台上的小物体A、B通过轻弹簧连接,并随转台一起匀速转动,A、B的质量分别为m、2m,A、B与转台的动摩擦因数都为μ,A、B离转台中心的距离分别为1.5r、r,已知弹簧的原长为1.5r,劲度系数为k,设本题中的最大静摩擦力等于滑动摩擦力,以下说法中正确的是( )
如图所示,水平转台上的小物体A、B通过轻弹簧连接,并随转台一起匀速转动,A、B的质量分别为m、2m,A、B与转台的动摩擦因数都为μ,A、B离转台中心的距离分别为1.5r、r,已知弹簧的原长为1.5r,劲度系数为k,设本题中的最大静摩擦力等于滑动摩擦力,以下说法中正确的是( )
 如图所示,水平转台上的小物体A、B通过轻弹簧连接,并随转台一起匀速转动,A、B的质量分别为m、2m,A、B与转台的动摩擦因数都为μ,A、B离转台中心的距离分别为1.5r、r,已知弹簧的原长为1.5r,劲度系数为k,设本题中的最大静摩擦力等于滑动摩擦力,以下说法中正确的是( )
如图所示,水平转台上的小物体A、B通过轻弹簧连接,并随转台一起匀速转动,A、B的质量分别为m、2m,A、B与转台的动摩擦因数都为μ,A、B离转台中心的距离分别为1.5r、r,已知弹簧的原长为1.5r,劲度系数为k,设本题中的最大静摩擦力等于滑动摩擦力,以下说法中正确的是( )| A. | 当B受到的摩擦力为0时,转台转动的角速度为$\sqrt{\frac{k}{m}}$ | |
| B. | 当A受到的摩擦力为0时,转台转动的角速度为$\sqrt{\frac{2k}{3m}}$ | |
| C. | 当B刚好要滑动时,转台转动的角速度为$\sqrt{\frac{k}{2m}+\frac{μg}{2r}}$ | |
| D. | 当A刚好要滑动时,转台转动的角速度为$\sqrt{\frac{2k}{3m}+\frac{2μg}{3r}}$ |
11.如图所示电路中,电源内阻r=R1=R2=R3.开关K接通后流过R1的电流是K接通前的( )


| A. | $\frac{6}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{2}$ |
1.一定质量的理想气体,当它的温度发生变化时,它的( )
| A. | 压强一定改变 | B. | 体积一定改变 | ||
| C. | 内能一定改变 | D. | 压强与体积可能都不会改变 |
5.有关热学,下列说法正确的是( )
| A. | 甲分子固定不动,乙分子从很远处向甲靠近到不能再靠近的过程中,分子间的分子势能是先减小后增大 | |
| B. | 一定质量的理想气体在体积不变的条件下,吸收热量,内能一定增大,压强一定增大 | |
| C. | 已知阿伏伽德罗常数为NA,水的摩尔质量为M,标准状况下水蒸气的密度为ρ(均为国际单位制单位),则1个水分子的体积是$\frac{M}{{ρ{N_A}}}$ | |
| D. | 自然界进行的涉及热现象的宏观过程都具有方向性,是不可逆的 | |
| E. | 随着科学技术的发展,人类终会制造出效率为100%的热机 |
12. 如图所示,条形磁铁放在水平桌面上,在其中正中央的上方固定一根长直导线,导线与磁铁垂直,现给导线通一垂直纸面向外的电流,则( )
如图所示,条形磁铁放在水平桌面上,在其中正中央的上方固定一根长直导线,导线与磁铁垂直,现给导线通一垂直纸面向外的电流,则( )
 如图所示,条形磁铁放在水平桌面上,在其中正中央的上方固定一根长直导线,导线与磁铁垂直,现给导线通一垂直纸面向外的电流,则( )
如图所示,条形磁铁放在水平桌面上,在其中正中央的上方固定一根长直导线,导线与磁铁垂直,现给导线通一垂直纸面向外的电流,则( )| A. | 磁铁对桌面的压力减小,受桌面的摩擦力作用 | |
| B. | 磁铁对桌面的压力减小,不受到桌面的摩擦力作用 | |
| C. | 磁铁对桌面的压力增大,不受桌面的摩擦力作用 | |
| D. | 磁铁对桌面的压力增大,受到桌面的摩擦力作用 |
 如图所示为正弦式交电流的电压u随时间t变化的图象,由图可知,该交变电流的电压的有效值为36V,频率为50Hz.
如图所示为正弦式交电流的电压u随时间t变化的图象,由图可知,该交变电流的电压的有效值为36V,频率为50Hz.