题目内容
4.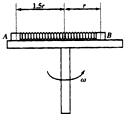 如图所示,水平转台上的小物体A、B通过轻弹簧连接,并随转台一起匀速转动,A、B的质量分别为m、2m,A、B与转台的动摩擦因数都为μ,A、B离转台中心的距离分别为1.5r、r,已知弹簧的原长为1.5r,劲度系数为k,设本题中的最大静摩擦力等于滑动摩擦力,以下说法中正确的是( )
如图所示,水平转台上的小物体A、B通过轻弹簧连接,并随转台一起匀速转动,A、B的质量分别为m、2m,A、B与转台的动摩擦因数都为μ,A、B离转台中心的距离分别为1.5r、r,已知弹簧的原长为1.5r,劲度系数为k,设本题中的最大静摩擦力等于滑动摩擦力,以下说法中正确的是( )| A. | 当B受到的摩擦力为0时,转台转动的角速度为$\sqrt{\frac{k}{m}}$ | |
| B. | 当A受到的摩擦力为0时,转台转动的角速度为$\sqrt{\frac{2k}{3m}}$ | |
| C. | 当B刚好要滑动时,转台转动的角速度为$\sqrt{\frac{k}{2m}+\frac{μg}{2r}}$ | |
| D. | 当A刚好要滑动时,转台转动的角速度为$\sqrt{\frac{2k}{3m}+\frac{2μg}{3r}}$ |
分析 当A、B受到的摩擦力为0时,由弹簧弹力提供向心力,根据胡克定律以及向心力公式列式求解,当A、B刚好要滑动时,摩擦力达到最大静摩擦力,弹簧弹力与静摩擦力的合力提供向心力,根据胡克定律以及向心力公式列式求解即可.
解答 解:A、当B受到的摩擦力为0时,由弹簧弹力提供向心力,则有k(1.5r+r-1.5r)=2mω2r
解得:$ω=\sqrt{\frac{k}{2m}}$,故A错误;
B、当A受到的摩擦力为0时,由弹簧弹力提供向心力,则有k(1.5r+r-1.5r)=mω2•1.5r
解得:$ω=\sqrt{\frac{2k}{3m}}$,故B正确;
C、当B刚好要滑动时,摩擦力达到最大静摩擦力,弹簧弹力与静摩擦力的合力提供向心力,则有:k(1.5r+r-1.5r)+μ•2mg=2mω2r
解得:ω=$\sqrt{\frac{k}{2m}+\frac{μg}{r}}$,故C错误;
D、当A刚好要滑动时,摩擦力达到最大静摩擦力,弹簧弹力与静摩擦力的合力提供向心力,则有k(1.5r+r-1.5r)+μmg=mω2•1.5r,
解得:$ω=\sqrt{\frac{2k}{3m}+\frac{2μg}{3r}}$,故D正确.
故选:BD
点评 本题主要考查了胡克定律以及向心力公式的直接应用,知道当A、B刚好要滑动时,摩擦力达到最大静摩擦力,弹簧弹力与静摩擦力的合力提供向心力,明确向心力的来源是解题的关键.

练习册系列答案
相关题目
15.某同学坐在火车甲上,以火车为参考系,看到乙、丙两列火车的运动方向相反.如果以地面为参考系,那么,关于三列火车的运动情况的下列说法中肯定错误的是( )
| A. | 甲、乙火车同向行驶,丙火车反向行驶 | |
| B. | 甲、乙、丙火车都在同向行驶 | |
| C. | 甲、乙火车反向行驶,丙火车静止不动 | |
| D. | 甲、乙火车同向行驶,丙火车静止不动 |
19.用接线板连接一台1500W的电饭锅,某同学在使用时发现连接线板的导线非常明显的发热现象,为了解决这个问题,应采用的措施是( )
| A. | 接线板导线换粗一些 | B. | 让电饭锅间歇工作 | ||
| C. | 停用家里的其它用电器 | D. | 家用电路的保险丝换粗一些 |
9.下列叙述正确的是( )
| A. | 外界对物体做功,物体的内能一定增加 | |
| B. | 热量不能由低温物体传递到高温物体 | |
| C. | 温度升高,物体内每个分子的热运动速率都增大 | |
| D. | 自然界中进行的涉及热现象的宏观过程都具有方向性 |
14.关于宇宙速度与卫星做圆周运动的运行速度.下面说法正确的是( )
| A. | 所有人造地球卫星在圆周上飞行速度都大于7.9m/s | |
| B. | 所有人造地球卫星飞行速度都小于7.9m/s | |
| C. | 所有人造地球卫星在地面的发射速度都大于7.9m/s | |
| D. | 所有人造地球卫星,在地面的发射速度都小于11.2m/s |
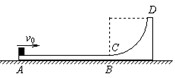 竖直平面内的轨道ABCD由水平滑道AB与光滑的四分之一圆弧滑道CD组成,AB恰与圆弧CD在C点相切,轨道放在光滑的水平面上,如图所示,已知轨道质量M=2kg处于静止,AB=1m,圆弧轨道半径R=2.8m,现有一个质量m=1kg的小物块从平台以速度V0从A端滑上,小物块与小车水平轨道间的动摩擦因数μ=0.4,(g取10m/s2).
竖直平面内的轨道ABCD由水平滑道AB与光滑的四分之一圆弧滑道CD组成,AB恰与圆弧CD在C点相切,轨道放在光滑的水平面上,如图所示,已知轨道质量M=2kg处于静止,AB=1m,圆弧轨道半径R=2.8m,现有一个质量m=1kg的小物块从平台以速度V0从A端滑上,小物块与小车水平轨道间的动摩擦因数μ=0.4,(g取10m/s2).
 如图,河宽L=60m,一只小船在河的正中央航行,经过O点时发现在距船S=40m的下游有一瀑布,为了使小船在A点安全靠岸,在O点立即调整好船头的指向,不至被冲进瀑布中.若河水的流速大小恒为5m/s,则小船的最小航行速率为3m/s.若河水的流速与到河岸的最短距离x成正比,即v水=kx(x≤$\frac{L}{2}$,k为一常量),小船在O点调整船头垂直河岸,让小船保持航行速率不变到达A点,则小船在平行河岸方向做匀减速运动.
如图,河宽L=60m,一只小船在河的正中央航行,经过O点时发现在距船S=40m的下游有一瀑布,为了使小船在A点安全靠岸,在O点立即调整好船头的指向,不至被冲进瀑布中.若河水的流速大小恒为5m/s,则小船的最小航行速率为3m/s.若河水的流速与到河岸的最短距离x成正比,即v水=kx(x≤$\frac{L}{2}$,k为一常量),小船在O点调整船头垂直河岸,让小船保持航行速率不变到达A点,则小船在平行河岸方向做匀减速运动. 如图所示,有一固定的光滑绝缘水平平台,平台右端B与水平传送带平滑相接,传送带长L=4m.一质量为m=0.5kg、带电量为q=+2×10-3C的滑块放在水平平台上.平台上有一根轻质弹簧左端固定,右端与滑块接触但不连接.现将滑块从A处由静止释放,无电且传送带不动时滑块恰能到达传送带右端C点.已知弹簧始终在弹性限度内,滑块到达B点前已与弹簧完全脱离,滑块与传送带间的动摩擦因数为μ=0.20,g取l0m/s2.求:
如图所示,有一固定的光滑绝缘水平平台,平台右端B与水平传送带平滑相接,传送带长L=4m.一质量为m=0.5kg、带电量为q=+2×10-3C的滑块放在水平平台上.平台上有一根轻质弹簧左端固定,右端与滑块接触但不连接.现将滑块从A处由静止释放,无电且传送带不动时滑块恰能到达传送带右端C点.已知弹簧始终在弹性限度内,滑块到达B点前已与弹簧完全脱离,滑块与传送带间的动摩擦因数为μ=0.20,g取l0m/s2.求: