��Ŀ����
8�� ��ͼ����X���Ϸ���y��0����������I��0��x��d���������3d��x��3d���ڷֱ������ǿ�ų����Ÿ�Ӧǿ�ȴ�С��ȣ�����ֱ��Oxyƽ��ָ���⣬�����������ų��ֲ�������Ϊm���������q��q��0�������Ӵ�y���ϵ�P����������I�����ٶȴ�СΪv0��������X��������֪���ӵ�������II���ұ߽�ʱǡ��ͬʱ����X�ᣬ���ٶȷ�����X�᷽��ֱ���������ӵ���������
��ͼ����X���Ϸ���y��0����������I��0��x��d���������3d��x��3d���ڷֱ������ǿ�ų����Ÿ�Ӧǿ�ȴ�С��ȣ�����ֱ��Oxyƽ��ָ���⣬�����������ų��ֲ�������Ϊm���������q��q��0�������Ӵ�y���ϵ�P����������I�����ٶȴ�СΪv0��������X��������֪���ӵ�������II���ұ߽�ʱǡ��ͬʱ����X�ᣬ���ٶȷ�����X�᷽��ֱ���������ӵ�����������1����ǿ�ų��ĴŸ�Ӧǿ�ȴ�С��
��2�����Ӵ���������I���뿪����II��������ʱ�䣿
���� ��1�������ڴų���������Բ���˶����ڴų���������ֱ���˶������������˶��Ĺ켣���ɼ��ι�ϵ�õ��켣��Ӧ��Բ�ĽǺ켣�뾶����ţ�ٵڶ����ɿ����B��
��2���ڹ켣��Ӧ��Բ�ĽǺ����ڣ�����ڴų����˶���ʱ�䣬�ɼ��ι�ϵ�õ��ų����˶���λ�ƴ�С��������˶�ʱ�䣬�Ӷ��õ���ʱ�䣮
��� �⣺��1�������ڴų���������Բ���˶����������˶��İ뾶ΪR�������ڴų����˶�����Ӧ��Բ�ĽǷֱ�Ϊ�����£����ӵ��˶��켣��ͼ��ʾ���ɼ��ι�ϵ�ã�
Rsin��=d
R-Rcos��=d
������x���������룬��ֱx�᷽����������У�
��+��=90��
��� ��=30�㡢��=60�㣬R=2d
�����ڴų���������Բ���˶��������������ṩ���������ã�
qvB=m$\frac{{v}_{0}^{2}}{R}$
�� B=$\frac{m{v}_{0}}{2dq}$
��2�������ڴų���������Բ���˶�����ΪT����T=$\frac{2��R}{v0}$=$\frac{4��d}{v0}$
�����������ų��������˶�����ʱ�䣺t1=$\frac{1}{4}$T=$\frac{��d}{v0}$
�������ų��������˶���ʱ�䣺t2=$\frac{\frac{d}{cos��}}{{v}_{0}}$=$\frac{2\sqrt{3}d}{3{v}_{0}}$
���Ӵ���������I���뿪����II��������ʱ�䣺t=t1+t2=$\frac{��d}{v0}$+$\frac{2\sqrt{3}d}{3{v}_{0}}$��
��
��1����ǿ�ų��ĴŸ�Ӧǿ�ȴ�С��$\frac{m{v}_{0}}{2dq}$��
��2�����Ӵ���������I���뿪����II��������ʱ��Ϊ$\frac{��d}{v0}$+$\frac{2\sqrt{3}d}{3{v}_{0}}$��
���� �����ڴų���Բ���˶����ͣ��ؼ�Ҫȷ���������˶��Ĺ켣�����������ѧ֪ʶ�����ؽǶȺ켣�뾶��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�ٽ����δ��۹��������һ��̧������һ�˴�Լ5cm�������������һľ�飬��ͼ��ʾ��ȷ��װ�õ��ȹ��ԣ�ʹһ��С�������ƽ���ع������ι�������Ӵ���
�ڲ�ù��ˮƽ���ֵij���Ϊ1m��
������б�����ij���ͷ�С�����ͷŸ߶ȣ����ˮƽ�����������������ˮƽ��ʱ����������������յ�ʱ��ͣ���������¼���ʱ�䣬����С����ˮƽ����ϵ����ʣ����������ݼ��㴦���������±���
�ܰ�����ľ��ֱ��ƶ�����б�����$\frac{1}{2}$����$\frac{1}{3}$����ʹ�����б�Ƕ������ظ�����ۣ��ֱ�õ�2��3�������ݣ�
�ݰ�ľ���ƶ�����б�����$\frac{1}{2}$�������ϸı��ͷ�λ�ã��ظ�����ۣ��õ���4�μ��Ժ����ʵ�����ݣ�
| ������� | �ͷŸ߶�h��m�� | ʱ��t/��s�� | v2 |
| 1 | 0.05 | 1.03 | 0.94 |
| 2 | 0.05 | 1.02 | 0.96 |
| 3 | 0.05 | 1.02 | 0.96 |
| 4 | 0.01 | 2.20 | 0.20 |
| 5 | 0.02 | 1.70 | |
| 6 | 0.03 | 1.30 | 0.59 |
| 7 | 0.04 | 1.14 | 0.77 |
| 8 | �� |
��1������ݲ��������5��ʵ���������ݣ�����v2=0.35m2/s2��
��2��д����С��ͬѧ���ǰ����ʵ���Ŀ����̽�����ܺ������ת���Ƿ���б������йأ�
��3����ʵ���п��ܲ�������ԭ������д�����������Ȳ�����ʱ�����
��3��Ħ��������ʱ��������������������Ȳ����ȣ���ֻҪ�������ɵ÷֣�
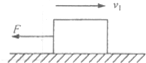 ��ˮƽ������С��龭����ͼ��ʾ��λ��ʱ���ٶȴ�СΪv1������ˮƽ���ң���������С���ʩ��ˮƽ����ĺ���F������һ��ʱ���С����ٴλص�ͼʾλ�ã��ٶȴ�СΪv2������ˮƽ������v2��v1����֪F=kmg����С�����ˮƽ����֮��Ķ�Ħ������Ϊ��������
��ˮƽ������С��龭����ͼ��ʾ��λ��ʱ���ٶȴ�СΪv1������ˮƽ���ң���������С���ʩ��ˮƽ����ĺ���F������һ��ʱ���С����ٴλص�ͼʾλ�ã��ٶȴ�СΪv2������ˮƽ������v2��v1����֪F=kmg����С�����ˮƽ����֮��Ķ�Ħ������Ϊ��������| A�� | $\frac{{v}_{1}^{2}+{v}_{2}^{2}}{k��{v}_{1}^{2}-{v}_{2}^{2}��}$ | B�� | $\frac{k��{v}_{1}^{2}+{v}_{2}^{2}��}{{v}_{1}^{2}-{v}_{2}^{2}}$ | ||
| C�� | $\frac{{v}_{1}^{2}-{v}_{2}^{2}}{k��{v}_{1}^{2}+{v}_{2}^{2}��}$ | D�� | $\frac{k��{v}_{1}^{2}-{v}_{2}^{2}��}{{v}_{1}^{2}+{v}_{2}^{2}}$ |
| A�� | �����������еĦ�1������Ц�1=��2+��3 | |
| B�� | �����������еĦ�1��С�����Ц�1=$\frac{{��}_{2}{��}_{3}}{{��}_{2}+{��}_{3}}$ | |
| C�� | �����������еĦ�1������Ц�1=��0 | |
| D�� | �����������еĦ�1��С�����Ц�1=��0 |
| A�� | �������������˶��Ĺ����У�����ʼ�մ��ڳ���״̬ | |
| B�� | �������������˶��Ĺ����У�����ʼ�մ���ʧ��״̬ | |
| C�� | �������뿪�ֵ�˲�䣬����ļ��ٶȴ����������ٶ� | |
| D�� | �������뿪�ֵ�˲�䣬�ֵļ��ٶȴ����������ٶ� |

 ��ͼ��ʾ��ֱ��OA��y��ɦ�=30��ǣ���AOAy��Χ������y�Ḻ�������ǿ�糡����AOx��Χ����һ�������������ǿ�ų����ôų�����ĴŸ�Ӧǿ��B=0.2T������ֱֽ�����һ�����������q=+2��10-14C����y��m=4��10-20kg������y���ϵ�ij�����ٶ�v0��ֱ��y�������ǿ�糡�������ٶ�v=3��104m/s��ֱ����ֱ��OA���˶��о������δų�����������ִ�ֱ����x�ᣮ�����������������������λ��Ч���֣�
��ͼ��ʾ��ֱ��OA��y��ɦ�=30��ǣ���AOAy��Χ������y�Ḻ�������ǿ�糡����AOx��Χ����һ�������������ǿ�ų����ôų�����ĴŸ�Ӧǿ��B=0.2T������ֱֽ�����һ�����������q=+2��10-14C����y��m=4��10-20kg������y���ϵ�ij�����ٶ�v0��ֱ��y�������ǿ�糡�������ٶ�v=3��104m/s��ֱ����ֱ��OA���˶��о������δų�����������ִ�ֱ����x�ᣮ�����������������������λ��Ч���֣�