题目内容
12. 如图所示,半径为2R的四分之一圆弧与半径为R的光滑半圆在B点相连接,C与A点等高,一个质量为m的小球从A点由静止释放,恰好到达与圆心O等高的D点.求:
如图所示,半径为2R的四分之一圆弧与半径为R的光滑半圆在B点相连接,C与A点等高,一个质量为m的小球从A点由静止释放,恰好到达与圆心O等高的D点.求:(1)摩擦力对小球所做的功是多少?
(2)假设AEB段摩擦力做功不变,小球刚过B点时对轨道的压力是多少?
(3)假设AEB段摩擦力做功不变,在A点给小球不同的速度,它将始终不脱离轨道运动,并能通过C点做平抛运动,当落点E到C点的竖直距离最大时,求A点的速度v0是多少?
分析 (1)从A到D有动能定理求的摩擦力做功;
(2)从A到B有动能定理求的到达B点速度,有牛顿第二定律求的作用力;
(3)从C点做平抛运动,求出竖直方向的高度,利用数学知识即可判断
解答 解:(1)摩擦力所做的共为W,则有:
mg•2R-W-mgR=0-0
W=-mgR
(2)根据题意有:
mg$•2R-W=\frac{1}{2}{mv}_{B}^{2}$
由牛顿第二定律有:F-mg=$\frac{{mv}_{B}^{2}}{R}$
解得:F=3mg
有牛顿第三定律可知,对轨道的压力为3mg
(3)设经过C点的速度为vC
x=vCt
$y=\frac{1}{2}g{t}^{2}$
x2+y2=4R2
得:$y=\frac{\sqrt{{v}_{C}^{4}+4{g}^{2}{R}^{2}}{-v}_{C}^{2}}{g}$
可知vC越小,y越大,最小是刚好能通过C点,
恰能通过C点则有:mg=$\frac{{mv}_{C}^{2}}{R}$
$mg•2R-W-mg•2R=\frac{1}{2}{mv}_{C}^{2}-\frac{1}{2}{mv}_{0}^{2}$
解得:${v}_{0}=\sqrt{3gR}$
答:(1)摩擦力对小球所做的功是-mgR
(2)假设AEB段摩擦力做功不变,小球刚过B点时对轨道的压力是3mg
(3)A点的速度v0是$\sqrt{3gR}$
点评 本题除了运用动能定理、平抛运动的规律之外,关键根据这些规律得到x的表达式,运用数学知识求极值,是常用的函数法,要学会运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2. 如图所示,匝数为10的矩形线框处在磁感应强度B=$\sqrt{2}$T的匀强磁场中,绕垂直磁场的轴以恒定角速度ω=10rad/s在匀强磁场中转动,线框电阻不计,面积为0.4m2,线框通过滑环与一理想自藕变压器的原线圈相连,副线圈接有一只灯泡L(4W,100Ω)和滑动变阻器,已知图示状况下灯泡正常发光,电流表视为理想电表,则下列说法正确的是( )
如图所示,匝数为10的矩形线框处在磁感应强度B=$\sqrt{2}$T的匀强磁场中,绕垂直磁场的轴以恒定角速度ω=10rad/s在匀强磁场中转动,线框电阻不计,面积为0.4m2,线框通过滑环与一理想自藕变压器的原线圈相连,副线圈接有一只灯泡L(4W,100Ω)和滑动变阻器,已知图示状况下灯泡正常发光,电流表视为理想电表,则下列说法正确的是( )
 如图所示,匝数为10的矩形线框处在磁感应强度B=$\sqrt{2}$T的匀强磁场中,绕垂直磁场的轴以恒定角速度ω=10rad/s在匀强磁场中转动,线框电阻不计,面积为0.4m2,线框通过滑环与一理想自藕变压器的原线圈相连,副线圈接有一只灯泡L(4W,100Ω)和滑动变阻器,已知图示状况下灯泡正常发光,电流表视为理想电表,则下列说法正确的是( )
如图所示,匝数为10的矩形线框处在磁感应强度B=$\sqrt{2}$T的匀强磁场中,绕垂直磁场的轴以恒定角速度ω=10rad/s在匀强磁场中转动,线框电阻不计,面积为0.4m2,线框通过滑环与一理想自藕变压器的原线圈相连,副线圈接有一只灯泡L(4W,100Ω)和滑动变阻器,已知图示状况下灯泡正常发光,电流表视为理想电表,则下列说法正确的是( )| A. | 此时原副线圈的匝数比为2:1 | |
| B. | 此时电流表的示数为0.4A | |
| C. | 若将自耦变压器触头向下滑动,灯泡会变暗 | |
| D. | 若将滑动变阻器滑片向上移动,则电流表示数增大 |
20. 如图所示,等腰直角三角形斜面OCD由不同材料A、B拼接而成,P为两种材料在CD边上的交点,且DP>CP.现让OD边水平放置,让小物块从C滑到D;然后将OC边水平放置,再让小物块从D滑到C,小物块两次滑动经过P点的时间相同.下列说法正确的是( )
如图所示,等腰直角三角形斜面OCD由不同材料A、B拼接而成,P为两种材料在CD边上的交点,且DP>CP.现让OD边水平放置,让小物块从C滑到D;然后将OC边水平放置,再让小物块从D滑到C,小物块两次滑动经过P点的时间相同.下列说法正确的是( )
 如图所示,等腰直角三角形斜面OCD由不同材料A、B拼接而成,P为两种材料在CD边上的交点,且DP>CP.现让OD边水平放置,让小物块从C滑到D;然后将OC边水平放置,再让小物块从D滑到C,小物块两次滑动经过P点的时间相同.下列说法正确的是( )
如图所示,等腰直角三角形斜面OCD由不同材料A、B拼接而成,P为两种材料在CD边上的交点,且DP>CP.现让OD边水平放置,让小物块从C滑到D;然后将OC边水平放置,再让小物块从D滑到C,小物块两次滑动经过P点的时间相同.下列说法正确的是( )| A. | A、B材料与小物块间的动摩擦因数相同 | |
| B. | 两次滑动中物块到达底端时的速率相等 | |
| C. | 两次滑动中物块到达P点时的速度相等 | |
| D. | 两次滑动中物块到达底端时克服摩擦做的功相等 |
7.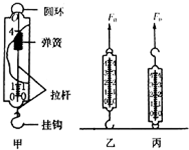 实验室常用的弹簧测力计如图甲所示,有挂钩的拉杆与弹簧相连,并固定在外壳一端O上,外壳上固定一个圆环,可以认为弹簧测力计的总质量主要集中在外壳(重量为G)上,弹簧和拉杆的质量忽略不计.再将该弹簧测力计以两种方式固定于地面上,如图乙、丙所示,分别用恒力F0竖直向上拉弹簧测力计,静止时弹簧测力计的读数为( )
实验室常用的弹簧测力计如图甲所示,有挂钩的拉杆与弹簧相连,并固定在外壳一端O上,外壳上固定一个圆环,可以认为弹簧测力计的总质量主要集中在外壳(重量为G)上,弹簧和拉杆的质量忽略不计.再将该弹簧测力计以两种方式固定于地面上,如图乙、丙所示,分别用恒力F0竖直向上拉弹簧测力计,静止时弹簧测力计的读数为( )
 实验室常用的弹簧测力计如图甲所示,有挂钩的拉杆与弹簧相连,并固定在外壳一端O上,外壳上固定一个圆环,可以认为弹簧测力计的总质量主要集中在外壳(重量为G)上,弹簧和拉杆的质量忽略不计.再将该弹簧测力计以两种方式固定于地面上,如图乙、丙所示,分别用恒力F0竖直向上拉弹簧测力计,静止时弹簧测力计的读数为( )
实验室常用的弹簧测力计如图甲所示,有挂钩的拉杆与弹簧相连,并固定在外壳一端O上,外壳上固定一个圆环,可以认为弹簧测力计的总质量主要集中在外壳(重量为G)上,弹簧和拉杆的质量忽略不计.再将该弹簧测力计以两种方式固定于地面上,如图乙、丙所示,分别用恒力F0竖直向上拉弹簧测力计,静止时弹簧测力计的读数为( )| A. | 乙图读数F0-G,丙图读数F0+G | B. | 乙图读数F0+G,丙图读数F0-G | ||
| C. | 乙图读数F0,丙图读数F0-G | D. | 乙图读数F0-G,丙图读数F0 |
 如图所示,在真空中相距为L=0.2m的足够长金属导轨MN和PQ与水平方向成α=37°倾斜放置,长度也均为L的质量为m1=0.1kg的金属棒ab 和质量为m2=0.2kg的金属棒cd,通过固定在金属棒两端的金属轻滑环套在套在导轨上,虚线OO′上方的匀强磁场的方向垂直于斜面向上,虚线OO′下方的匀强磁场的方向平行于斜面向上,两处的匀强磁场的磁感应强度大小均为B=1T.ab两端的滑环是光滑的,cd两端的滑环与导轨间的动摩擦因数为0.25,两金属棒在导轨间的电阻均为R0=0.5Ω,导轨和滑环的电阻不计,现金属棒ab在沿斜面向上的外力F的作用下,从静止开始沿导轨向上做加速度为a=2m/s2的匀加速直线运动,在金属棒ab刚开始运动的同时,金属棒cd也由静止释放.sin37°=0.6,cos37°=0.8,重力加速度为g=10m/s2.求:
如图所示,在真空中相距为L=0.2m的足够长金属导轨MN和PQ与水平方向成α=37°倾斜放置,长度也均为L的质量为m1=0.1kg的金属棒ab 和质量为m2=0.2kg的金属棒cd,通过固定在金属棒两端的金属轻滑环套在套在导轨上,虚线OO′上方的匀强磁场的方向垂直于斜面向上,虚线OO′下方的匀强磁场的方向平行于斜面向上,两处的匀强磁场的磁感应强度大小均为B=1T.ab两端的滑环是光滑的,cd两端的滑环与导轨间的动摩擦因数为0.25,两金属棒在导轨间的电阻均为R0=0.5Ω,导轨和滑环的电阻不计,现金属棒ab在沿斜面向上的外力F的作用下,从静止开始沿导轨向上做加速度为a=2m/s2的匀加速直线运动,在金属棒ab刚开始运动的同时,金属棒cd也由静止释放.sin37°=0.6,cos37°=0.8,重力加速度为g=10m/s2.求: 如图,半径为R的光滑圆形轨道固定在竖直面内.可当做质点的小球A、B质量分别为m、3m,A球从左边与圆心等高处由静止开始沿轨道下滑,与静止于轨道最低点的B球相撞,第一次碰撞后A、B球能达到的最大高度相同,碰撞中无机械能损失.重力加速度为g.试求:
如图,半径为R的光滑圆形轨道固定在竖直面内.可当做质点的小球A、B质量分别为m、3m,A球从左边与圆心等高处由静止开始沿轨道下滑,与静止于轨道最低点的B球相撞,第一次碰撞后A、B球能达到的最大高度相同,碰撞中无机械能损失.重力加速度为g.试求: 如图所示,光滑水平面左端的固定装置P能根据需要发射和接收质量m=0.1kg、速度为v0=8m/s的小球;右边用一长为L=2.45m的不可伸长细线系一质量M=0.3kg的小球B,绳另一端固定于悬点,起初绳拉直,小球B静止于地面上且对地面的压力恰为零.某时刻让P发射一小球与静止的小球B发生碰撞,假定以后每当小球B经最低点且向右运动时就有一发射小球与小球B碰撞,导致小球B摆动的最大高度逐渐增加,设每次碰撞均没有机械能损失,g=10m/s2.求:
如图所示,光滑水平面左端的固定装置P能根据需要发射和接收质量m=0.1kg、速度为v0=8m/s的小球;右边用一长为L=2.45m的不可伸长细线系一质量M=0.3kg的小球B,绳另一端固定于悬点,起初绳拉直,小球B静止于地面上且对地面的压力恰为零.某时刻让P发射一小球与静止的小球B发生碰撞,假定以后每当小球B经最低点且向右运动时就有一发射小球与小球B碰撞,导致小球B摆动的最大高度逐渐增加,设每次碰撞均没有机械能损失,g=10m/s2.求: