题目内容
19. 距地面高5m的水平直轨道上A、B两点相距2m,在B点用细线悬挂一小球,离地高度为h,如图.小车始终以4m/s的速度沿轨道匀速运动,经过A点时将随车携带的小球由轨道高度自由卸下,小车运动至B点时细线被轧断,最后两球同时落地.不计空气阻力,取重力加速度的大小g=10m/s2.可求得h等于( )
距地面高5m的水平直轨道上A、B两点相距2m,在B点用细线悬挂一小球,离地高度为h,如图.小车始终以4m/s的速度沿轨道匀速运动,经过A点时将随车携带的小球由轨道高度自由卸下,小车运动至B点时细线被轧断,最后两球同时落地.不计空气阻力,取重力加速度的大小g=10m/s2.可求得h等于( )| A. | 1.25 m | B. | 2.25 m | C. | 3.75 m | D. | 4.75 m |
分析 经过A点时将随车携带的小球由轨道高度自由卸下后,小球做平抛运动,小车运动至B点时细线被轧断,则B处的小球做自由落体运动,根据平抛运动及自由落体运动基本公式抓住时间关系列式求解.
解答 解:设轨道离地的高度为H,则知 H=5m
经过A点,将球自由卸下后,A球做平抛运动,则有:
H=$\frac{1}{2}$gt12
解得:t1=1s
小车从A点运动到B点的时间 t2=$\frac{{x}_{AB}}{v}$=$\frac{2}{4}$s=0.5s
因为两球同时落地,则细线被轧断后B处小球做自由落体运动的时间为 t3=t1-t2=1-0.5=0.5s
则 h=$\frac{1}{2}$gt22=$\frac{1}{2}$×10×0.52=1.25m
故选:A
点评 本题的关键要分析AB两球的运动情况,抓住同时落地时两球运动的时间关系,运用运动学规律分段研究.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.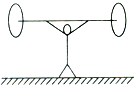 体育运动中包含着丰富的力学知识,如图所示,举重运动员举起质量为120kg的杠铃,双臂夹角为120°,取g=10m/s2,则运动员两臂对杠铃的作用力为( )
体育运动中包含着丰富的力学知识,如图所示,举重运动员举起质量为120kg的杠铃,双臂夹角为120°,取g=10m/s2,则运动员两臂对杠铃的作用力为( )
 体育运动中包含着丰富的力学知识,如图所示,举重运动员举起质量为120kg的杠铃,双臂夹角为120°,取g=10m/s2,则运动员两臂对杠铃的作用力为( )
体育运动中包含着丰富的力学知识,如图所示,举重运动员举起质量为120kg的杠铃,双臂夹角为120°,取g=10m/s2,则运动员两臂对杠铃的作用力为( )| A. | 750 N | B. | 800 N | C. | 1000 N | D. | 1200 N |
10.宇宙中存在一些质量相等且离其他恒星较远的四颗星组成的四星系统,通常可忽略其他星体对它们的引力作用.设四星系统中每个星体的质量均为m,半径均为R,四颗星稳定分布在边长为L的正方形的四个顶点上,其中L远大于R.已知万有引力常量为G.忽略星体自转效应,关于四星系统,下列说法正确的是( )
| A. | 四颗星圆周运动的轨道半径均为$\frac{L}{2}$ | |
| B. | 四颗星圆周运动的线速度均为 $\sqrt{\frac{Gm}{L}(2+\frac{\sqrt{2}}{4})}$ | |
| C. | 四颗星圆周运动的周期均为2π $\sqrt{\frac{2{L}^{3}}{(4+\sqrt{2})Gm}}$ | |
| D. | 四颗星表面的重力加速度均为G$\frac{m}{{R}^{2}}$ |
14.在双缝干涉实验中发现条纹太密,难以测量,可以采用的改善办法是( )
| A. | 改用波长较长的光(如红光)作入射光 | B. | 增大双缝到屏的距离 | ||
| C. | 减小双缝间距 | D. | 增大双缝间距 |
11. 如图所示,一木块质量为4kg,放在水平地面上,在水平力F作用下向右运动,水平地面AB段光滑,BC段粗糙,木块从A点运动到C点的v-t图象如图乙所示,则下列说法正确的是(g=10m/s2)( )
如图所示,一木块质量为4kg,放在水平地面上,在水平力F作用下向右运动,水平地面AB段光滑,BC段粗糙,木块从A点运动到C点的v-t图象如图乙所示,则下列说法正确的是(g=10m/s2)( )
 如图所示,一木块质量为4kg,放在水平地面上,在水平力F作用下向右运动,水平地面AB段光滑,BC段粗糙,木块从A点运动到C点的v-t图象如图乙所示,则下列说法正确的是(g=10m/s2)( )
如图所示,一木块质量为4kg,放在水平地面上,在水平力F作用下向右运动,水平地面AB段光滑,BC段粗糙,木块从A点运动到C点的v-t图象如图乙所示,则下列说法正确的是(g=10m/s2)( )| A. | 木块在BC段的摩擦力为0.1N | B. | 拉力在BC段做功为28J | ||
| C. | 在t=6s时,摩擦力的功率为8W | D. | 木块在BC段克服摩擦力做功为14J |
8.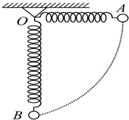 如图所示,一轻弹簧固定于O点,另一端系一小球,将小球从与悬点O在同一水平面且弹簧保持原长的A点无初速度释放,让它自由摆下,不计空气阻力,在小球由A点摆向最低点S的过程( )
如图所示,一轻弹簧固定于O点,另一端系一小球,将小球从与悬点O在同一水平面且弹簧保持原长的A点无初速度释放,让它自由摆下,不计空气阻力,在小球由A点摆向最低点S的过程( )
 如图所示,一轻弹簧固定于O点,另一端系一小球,将小球从与悬点O在同一水平面且弹簧保持原长的A点无初速度释放,让它自由摆下,不计空气阻力,在小球由A点摆向最低点S的过程( )
如图所示,一轻弹簧固定于O点,另一端系一小球,将小球从与悬点O在同一水平面且弹簧保持原长的A点无初速度释放,让它自由摆下,不计空气阻力,在小球由A点摆向最低点S的过程( )| A. | 小球做圆周运动 | B. | 弹簧弹性势能不变 | ||
| C. | 小球的机械能减少 | D. | 小球和弹簧组成的系统机械能减少 |
9.下列说法中正确的是( )
| A. | 能量的耗散从能量的转化角度反映出了自然界中的宏观过程具有方向性 | |
| B. | 空调机既能致热又能致冷,说明热传递不存在方向性 | |
| C. | 如果气体分子总数不变,而气体温度升高,气体分子的平均动能增大,因此压强必然增大 | |
| D. | 热量总是自发的从分子平均动能大的物体传递到分子平均动能小的物体 |
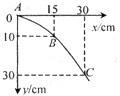 在“研究平抛运动”实验中:
在“研究平抛运动”实验中: 如图所示,质量为M的小车静止在光滑的水平面上,小车上AB部分是半径为R的四分之一光滑圆弧,BC部分是粗糙的水平面.今把质量为m的小物体从A点由静止释放,最终小物体与小车相对静止于B、C之间的D点,若B、D间的距离L,求
如图所示,质量为M的小车静止在光滑的水平面上,小车上AB部分是半径为R的四分之一光滑圆弧,BC部分是粗糙的水平面.今把质量为m的小物体从A点由静止释放,最终小物体与小车相对静止于B、C之间的D点,若B、D间的距离L,求