题目内容
4. 如图所示,物块A的质量为M,物块B、C的质量都是m,均可看作质点,且m<M<2m.三物块用轻绳通过滑轮连接.一轻弹簧下端固定在地面上,其上端与物块A相连,劲度系数为k,物块B与物块C的距离和物块C到地面的距离都是L.设物块A距滑轮足够远,不计一切摩擦阻力,开始时系统处于静止状态.求:
如图所示,物块A的质量为M,物块B、C的质量都是m,均可看作质点,且m<M<2m.三物块用轻绳通过滑轮连接.一轻弹簧下端固定在地面上,其上端与物块A相连,劲度系数为k,物块B与物块C的距离和物块C到地面的距离都是L.设物块A距滑轮足够远,不计一切摩擦阻力,开始时系统处于静止状态.求:(1)弹簧的形变量;
(2)若将轻弹簧剪断,物块A上升时的最大速度;
(3)将轻弹簧剪断后,物块A上升的最大高度(物块着地不反弹).
分析 (1)受力分析结合胡克定律求解形变量;
(2)A、B、C三物体系统机械能守恒.B、C下降L,A上升L时,A的速度达到最大,根据机械能列式求解;
(3)当C着地后,A、B二物体系统机械能守恒.B恰能着地,即B物体下降L时速度为零.
MgL-mgL=$\frac{1}{2}$(M+m)vm2解得M,分析m大小与M关系从而根据能量守恒求物块A上升的最大高度.
解答 解:(1)对A:F=2mg-Mg….①
根据胡克定律知:F=kx….②
由①②解得 x=$\frac{2mg-Mg}{k}$.
(2)A、B、C三物体系统机械能守恒.B、C下降L,A上升L时,A的速度达到最大.
2mgL-MgL=$\frac{1}{2}$(M+2m)vm2….③
由③解得vm=$\sqrt{\frac{2(2m-M)gL}{2m+M}}$…④
(3)当C着地后,A、B二物体系统机械能守恒.B恰能着地,即B物体下降L时速度为零.
MgL-mgL=$\frac{1}{2}$(M+m)vm2….⑤
由④⑤解得:M=$\sqrt{2}$m….
①若$\sqrt{2}$m<M<2m,B物体将不会着地.
Mgh-mgh=$\frac{1}{2}$(M+m) vm2….⑥
h=$\frac{(M+m){{v}_{m}}^{2}}{2(M-m)g}$
H1=L+h=$\frac{2MmL}{(2m+M)(M-m)}$⑦
②若M=$\sqrt{2}$m,B恰能着地,A物体再上升的高度等于L.
H2=2L
③若m<M<$\sqrt{2}$m,B物体着地后,A还会上升一段.设B落地的速度v
MgL-mgL=$\frac{1}{2}$(M+m)(vm2-v2) ….⑧
△h=$\frac{{v}^{2}}{2g}$….⑨
H3=2L+△h ⑩
由⑧⑨⑩得 H3=2L+$\frac{2(2{m}^{2}-{M}^{2})L}{(m+M)(2m+M)}$
答:(1)弹簧的形变量为$\frac{2mg-Mg}{k}$;
(2)若将轻弹簧剪断,物块A上升时的最大速度为$\sqrt{\frac{2(2m-M)gL}{2m+M}}$;
(3)将轻弹簧剪断后,物块A上升的最大高度为2L+$\frac{2(2{m}^{2}-{M}^{2})L}{(m+M)(2m+M)}$.
点评 该题是一道综合题,综合运用了机械能守恒定律以及功能关系,解决本题的关键熟练这些定理、定律的运用,注意分析质量关系即可.

 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 转台上放一质量为m的物体,它离轴的距离是R.如图,当物体随转台一起转动时,向心力由什么力提供( )
转台上放一质量为m的物体,它离轴的距离是R.如图,当物体随转台一起转动时,向心力由什么力提供( )| A. | 重力 | B. | 弹力 | C. | 静摩擦力 | D. | 滑动摩擦力 |
 如图所示,两个皮带轮顺时针转动,带动水平传送带以不变的速率v运行.将质量为m的物体A(可视为质点)轻轻放在传送带左端,经时间t后,A的速度变为v,再经过时间t后,到达传送带右端.则( )
如图所示,两个皮带轮顺时针转动,带动水平传送带以不变的速率v运行.将质量为m的物体A(可视为质点)轻轻放在传送带左端,经时间t后,A的速度变为v,再经过时间t后,到达传送带右端.则( )| A. | 物体A由传送带左端运动到右端的平均速度为$\frac{1}{2}$v | |
| B. | 物体A由传送带左端运动到右端的平均速度为$\frac{3}{4}$v | |
| C. | 传送带克服物体A对它的摩擦力所做的功为mv2 | |
| D. | 整个过程中系统因摩擦产生的内能为mv2 |

| A. | 若木块静止,则木块受到的静摩擦力大小等于mg,方向竖直向上 | |
| B. | 若木块静止,当F增大时,木块受到的静摩擦力随之增大 | |
| C. | 若木块沿墙壁向下运动,则墙壁对木块的摩擦力大小为μmg | |
| D. | 若开始时木块静止.当撤去F,木块沿墙壁下滑时,木块不受滑动摩擦力作用 |
| A. | 如果地球没有自转,只要采取适当的发射速度和发射角度,也可以发射地球同步卫星 | |
| B. | 小船在水速较小的河中横渡,并使船头始终垂直河岸航行,到达河中间时突然上游来大水使水流速度加快,则小船要用更长的时间才能到达对岸 | |
| C. | 一个物体以0.5g竖直下落了高度h,机械能减少0.5mgh | |
| D. | 无论宏观物体还是微观物体,无论高速运动还是低速运动,都可以运用牛顿运动规律处理 |
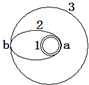 如图所示,是某次发射人造卫星的示意图,人造卫星先在半径为r的近地圆周轨道1上运动,然后改在椭圆轨道2上运动,最后在半径为7r的圆周轨道3上运动,a点是轨道1、2的交点,b点是轨道2、3的交点,人造卫星在轨道1上a点的速度为v1a,在轨道2上a点的速度为v2a,在轨道2上b点的速度为v2b,在轨道3上b点的速度为v3b,已知卫星在圆轨道运行时的引力势能为Ep=-$\frac{GMm}{r}$选择无穷远处为势能零点,r是卫星与中心天体的球心距,下列说法正确的是( )
如图所示,是某次发射人造卫星的示意图,人造卫星先在半径为r的近地圆周轨道1上运动,然后改在椭圆轨道2上运动,最后在半径为7r的圆周轨道3上运动,a点是轨道1、2的交点,b点是轨道2、3的交点,人造卫星在轨道1上a点的速度为v1a,在轨道2上a点的速度为v2a,在轨道2上b点的速度为v2b,在轨道3上b点的速度为v3b,已知卫星在圆轨道运行时的引力势能为Ep=-$\frac{GMm}{r}$选择无穷远处为势能零点,r是卫星与中心天体的球心距,下列说法正确的是( )| A. | 轨道1、2、3的周期之比为7$\sqrt{7}$:8:1 | |
| B. | v2a>v1a>v2b>v3b | |
| C. | v2a>v1a>v3b>v2b | |
| D. | 圆周轨道1和3上运行时,卫星和地球系统的机械能之比为1:14 |
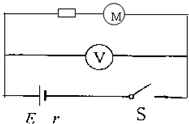 宜宾市小科学家协会的一位同学设计了一台玩具车,其内部结构的简化电路图如图所示.电源电动势为E,内阻r=1Ω,直流电动机M的线圈电阻R0=1Ω,与R=1Ω的保护电阻串联后接入电路中.电动机正常工作时,通过电动机的电流强度I=1A,电压表示数U=11V.求:
宜宾市小科学家协会的一位同学设计了一台玩具车,其内部结构的简化电路图如图所示.电源电动势为E,内阻r=1Ω,直流电动机M的线圈电阻R0=1Ω,与R=1Ω的保护电阻串联后接入电路中.电动机正常工作时,通过电动机的电流强度I=1A,电压表示数U=11V.求: 如图所示,斜面倾角为θ=30°,一弹簧下端与固定挡板连接,上端与一个质量为2kg的物体相连,物体在斜面上静止不动.弹簧原长为10cm,现在的长度为8cm.(g=10m/s2)
如图所示,斜面倾角为θ=30°,一弹簧下端与固定挡板连接,上端与一个质量为2kg的物体相连,物体在斜面上静止不动.弹簧原长为10cm,现在的长度为8cm.(g=10m/s2)