题目内容
8.在“探究”加速度与力、质量的关系的实验中,采用如图1所示的实验装置,小车及车中砝码的质量用M表示,盘及盘中砝码的质量用m表示,小车的加速度可由小车后拖动的纸 带由打点计时器打出的点计算出.
①当M与m的大小关系满足m<<M时,才可以认为绳对小车的拉力大小等于盘和盘中砝码的重力.
②一组同学在做加速度与质量的关系实验时,保持盘及盘中砝码的质量一定,改变小车及车中砝码的质量,测出相应的加速度.采用图象法处理数据.为了比较容易地检查出加速度a与质量M的关系,应该做a与$\frac{1}{M}$的图象.
③乙、丙同学用同一装置做实验,画出了各自得到的a-F图象如图2所示,两个同学做实验时的哪一个物理量取值不同小车及车中砝码的总质量M..
分析 要求在什么情况下才可以认为绳对小车的拉力大小等于盘和盘中砝码的重力,需求出绳子的拉力,而要求绳子的拉力,应先以整体为研究对象求出整体的加速度,再以M为研究对象求出绳子的拉力,通过比较绳对小车的拉力大小和盘和盘中砝码的重力的大小关系得出只有m<<M时才可以认为绳对小车的拉力大小等于盘和盘中砝码的重力.
反比例函数图象是曲线,而根据曲线很难判定出自变量和因变量之间的关系;正比例函数图象是过坐标原点的一条直线,就比较容易判定自变量和因变量之间的关系.
a-F图象的斜率等于物体的质量,故斜率不同则物体的质量不同.
解答 解:①以整体为研究对象有mg=(m+M)a
解得:a=$\frac{mg}{m+M}$,
以M为研究对象有绳子的拉力F=Ma=$\frac{mg}{M+\frac{m}{M}}$,
显然要有F=mg必有m+M=M,故有m<<M,即只有m<<M时才可以认为绳对小车的拉力大小等于盘和盘中砝码的重力.
②根据牛顿第二定律F=Ma,a与M成反比,而反比例函数图象是曲线,而根据曲线很难判定出自变量和因变量之间的关系,故不能作a-M图象;
a=$\frac{F}{M}$,故a与$\frac{1}{M}$成正比,而正比例函数图象是过坐标原点的一条直线,就比较容易判定自变量和因变量之间的关系,故应作a-$\frac{1}{M}$图象.
③由图可知在拉力相同的情况下a乙>a甲,
根据F=ma可得m=$\frac{F}{a}$,即a-F图象的斜率等于物体的质量,且m乙<m甲.故两人的实验中小车及车中砝码的总质量M不同.
故答案为:
①m<<M
②$\frac{1}{M}$;
③小车及车中砝码的总质量M.
点评 只要真正掌握了实验原理就能顺利解决此类实验题目,而实验步骤,实验数据的处理都与实验原理有关,故要加强对实验原理的学习和掌握.

 在如图所示的静电实验电路中,已知电容器的电容C1=C2=C,电源的电动势为E,内阻为r,伏特表的内阻为10kΩ,当电路达到稳定状态后,则( )
在如图所示的静电实验电路中,已知电容器的电容C1=C2=C,电源的电动势为E,内阻为r,伏特表的内阻为10kΩ,当电路达到稳定状态后,则( )| A. | 静电计上电势差为零 | B. | 伏特计上电势差为零 | ||
| C. | 电容器C1所带电量为CE | D. | 电容器C2所带电量为CE |
 在如图所示的交流电路中,保持电源电压一定,当交变电流的频率增大时,各电压表的求数将( )
在如图所示的交流电路中,保持电源电压一定,当交变电流的频率增大时,各电压表的求数将( )| A. | V1、V3增大,V2减小 | B. | V1不变,V2减小,V3增大 | ||
| C. | V1不变,V2增大,V3减小 | D. | V1、V2、V3都不变 |
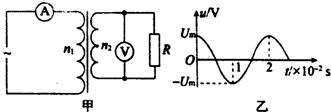
| A. | 通过R的电流iR随时间t的变化规律是iR=$\sqrt{2}$cos100πt(A) | |
| B. | 电压表V的示数为8V | |
| C. | 电流表A的示数为0.48A | |
| D. | 变压器的输入功率为8W |
 在一个电场中a、b、c、d四个点分别引入试探电荷时,电荷所受到的电场力F跟引入电荷量之间的函数关系如图所示,下列说法中正确的是( )
在一个电场中a、b、c、d四个点分别引入试探电荷时,电荷所受到的电场力F跟引入电荷量之间的函数关系如图所示,下列说法中正确的是( )| A. | 这个电场是匀强电场 | |
| B. | a、b、c、d四点的电场强度大小关系是Ed>Eb>Ec>Ea | |
| C. | a、b、c、d四点的电场强度大小关系是Eb>Ea>Ed>Ec | |
| D. | 无法比较以上四点的电场强度值 |
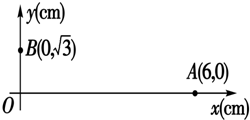 如图所示,在平面直角坐标系中,有方向平行于坐标平面的匀强电场,其中坐标原点O处的电势为0V,点A处的电势为6V,点B处的电势为3V,则
如图所示,在平面直角坐标系中,有方向平行于坐标平面的匀强电场,其中坐标原点O处的电势为0V,点A处的电势为6V,点B处的电势为3V,则 一光滑曲面的末端与一长L=1m的水平传送带相切,传送带离地面的高度h=1.25m,传送带的滑动摩擦因数μ=0.1,地面上有一个直径D=0.5m的圆形洞,洞口最左端的A点离传送带右端的水平距离S=1m,B点在洞口的最右端.传动轮作顺时针转动,使传送带以恒定的速度运动.现使某小物体从曲面上距离地面高度H处由静止开始释放,到达传送带上后小物体的速度恰好和传送带相同,并最终恰好由A点落入洞中.求:
一光滑曲面的末端与一长L=1m的水平传送带相切,传送带离地面的高度h=1.25m,传送带的滑动摩擦因数μ=0.1,地面上有一个直径D=0.5m的圆形洞,洞口最左端的A点离传送带右端的水平距离S=1m,B点在洞口的最右端.传动轮作顺时针转动,使传送带以恒定的速度运动.现使某小物体从曲面上距离地面高度H处由静止开始释放,到达传送带上后小物体的速度恰好和传送带相同,并最终恰好由A点落入洞中.求: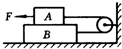 所受重力分别为G1和G2的滑块A,B,由绕过定滑轮的细绳相连后,叠放在水平桌面上,如图所示.已知A,B间的摩擦系数为μ1,B与桌面间的摩擦系数为μ2.问:
所受重力分别为G1和G2的滑块A,B,由绕过定滑轮的细绳相连后,叠放在水平桌面上,如图所示.已知A,B间的摩擦系数为μ1,B与桌面间的摩擦系数为μ2.问: