题目内容
9. 我国将于2022 年举办冬季奥运会,跳台滑雪是其中最具观赏性的项目之一.当滑雪板相对雪地速度较小时,滑雪板与雪地间的摩擦力较大,当滑雪板相对雪地速度较大时,滑雪板会把雪内的空气逼出来,在滑雪板与雪地间形成一个暂时的“气垫”,从而大大减小雪地对滑雪板的摩擦.假设滑雪者的速度超过4m/s 时,滑雪板与雪地间的动摩擦因数就会由μ1=0.25 变为μ2=0.125.如图所示,一运动员从倾角θ=37°的长直助滑道AB 的A 处由静止开始自由下滑,滑至末端B 后沿切线进入一半径为R=21m 的竖直光滑圆弧轨道BC,并从最低点C 沿水平方向飞出,最后落在水平地面上的D 点.不计空气阻力,AB 长度s=40.4m,C 与D 点的高度差h=3.2m,取g=10m/s2,sin37°=0.6,cos37°=0.8.求:
我国将于2022 年举办冬季奥运会,跳台滑雪是其中最具观赏性的项目之一.当滑雪板相对雪地速度较小时,滑雪板与雪地间的摩擦力较大,当滑雪板相对雪地速度较大时,滑雪板会把雪内的空气逼出来,在滑雪板与雪地间形成一个暂时的“气垫”,从而大大减小雪地对滑雪板的摩擦.假设滑雪者的速度超过4m/s 时,滑雪板与雪地间的动摩擦因数就会由μ1=0.25 变为μ2=0.125.如图所示,一运动员从倾角θ=37°的长直助滑道AB 的A 处由静止开始自由下滑,滑至末端B 后沿切线进入一半径为R=21m 的竖直光滑圆弧轨道BC,并从最低点C 沿水平方向飞出,最后落在水平地面上的D 点.不计空气阻力,AB 长度s=40.4m,C 与D 点的高度差h=3.2m,取g=10m/s2,sin37°=0.6,cos37°=0.8.求:(1)运动员到达B 时的速率;
(2)D 点与C 点的水平距离.
分析 (1)分别求得运动员速度在4m/s前后的合外力,进而由牛顿第二定律求得加速度,然后根据匀变速规律通过总位移为s求得末速度;
(2)通过BC段运动机械能守恒求得在C点的速度,然后根据平抛运动的位移公式求解水平位移.
解答 解:(1)运动员在速度v<4m/s时合外力F1=mgsinθ-μ1mgcosθ,故加速度${a}_{1}=\frac{{F}_{1}}{m}=gsinθ-{μ}_{1}gcosθ=4m/{s}^{2}$;
所以,运动员下滑${t}_{1}=\frac{4m/s}{{a}_{1}}=1s$,位移${s}_{1}=\frac{1}{2}{a}_{1}{{t}_{1}}^{2}=2m$后达到v0=4m/s;
之后,运动员的合外力F2=mgsinθ-μ2mgcosθ,故加速度${a}_{2}=\frac{{F}_{2}}{m}=gsinθ-{μ}_{2}gcosθ=5m/{s}^{2}$;
故由匀变速运动规律可得:$s-{s}_{1}={v}_{0}{t}_{2}+\frac{1}{2}{a}_{2}{{t}_{2}}^{2}$,所以,t2=3.2s,那么,运动员到达B 时的速率vB=v0+a2t2=20m/s;
(2)运动员在BC上运动只有重力做功,故机械能守恒,则有:$\frac{1}{2}m{{v}_{C}}^{2}=\frac{1}{2}m{{v}_{B}}^{2}+mgR(1-cosθ)$,所以,${v}_{C}=\sqrt{{{v}_{B}}^{2}+2gR(1-cosθ)}=22m/s$;
那么,运动员从C到D做平抛运动,设D 点与C 点的水平距离为x,故有:$h=\frac{1}{2}g{t}^{2}$,$x={v}_{C}t={v}_{C}\sqrt{\frac{2h}{g}}=17.6m$;
答:(1)运动员到达B 时的速率为20m/s;
(2)D 点与C 点的水平距离为17.6m.
点评 经典力学问题一般先对物体进行受力分析,求得合外力及运动过程做功情况,然后根据牛顿定律、动能定理及几何关系求解.

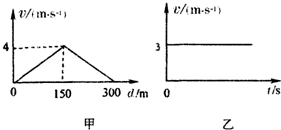 河中各点水速大小与各点到河岸的垂直距离的关系如图甲所示,船在静水中的速度与时间的关系如图乙所示,若要使船以最短时间渡河,下列说法中正确的是( )
河中各点水速大小与各点到河岸的垂直距离的关系如图甲所示,船在静水中的速度与时间的关系如图乙所示,若要使船以最短时间渡河,下列说法中正确的是( )| A. | 船渡河的最短时间60s | |
| B. | 船在行驶过程中,船头始终与河岸垂直 | |
| C. | 船航行的轨迹是一条直线 | |
| D. | 船在沿河岸方向相等时间内运动的位移越来越大 |
 如图所示,木块M上表面是水平的,当木块m置于M上,并与M一起沿固定的光滑斜面由静止开始下滑,在下滑过程中( )
如图所示,木块M上表面是水平的,当木块m置于M上,并与M一起沿固定的光滑斜面由静止开始下滑,在下滑过程中( )| A. | M对m的支持力对m做负功 | B. | M对m的摩擦力对m做负功 | ||
| C. | M对m的作用力做负功 | D. | M对m的作用力做正功 |
 中国运动员参加奥运蹦床比赛,取得骄人的成绩.运动员从接触蹦床至运动到最低点的过程中(不计空气阻力),下列说法正确的是( )
中国运动员参加奥运蹦床比赛,取得骄人的成绩.运动员从接触蹦床至运动到最低点的过程中(不计空气阻力),下列说法正确的是( )| A. | 运动员的机械能先增大后减小 | |
| B. | 运动员的动量先减小后增大 | |
| C. | 运动员所受重力的冲量小于运动员所受弹力的冲量 | |
| D. | 只有重力和蹦床弹力对运动员做功,运动员的机械能守恒 |

| A. | 甲图烧杯内是光的直线传播现象 | |
| B. | 甲、乙图说明凸透镜对光有会聚作用 | |
| C. | 甲、丙图说明凹透镜对光有发散作用 | |
| D. | 光需要杯内的烟雾来传递 |
| A. | 露珠成球形是由于液体表面张力的作用 | |
| B. | 气体温度不变,整体运动速度越大,其内能越大 | |
| C. | 食盐熔化过程中,温度保持不变,说明食盐是非晶体 | |
| D. | 温度越高,物体中分子无规则运动越剧烈 | |
| E. | 空调既能制热又能制冷,说明在不自发地条件下热传递方向可以逆向 |
 如图所示,质量为M的木块放在光滑的水平面上,质量为m的子弹以速度v0沿水平方向射中木块,并最终留在木块中与木块一起以速度v运动.已知当子弹相对木块静止时,木块前进距离为L,子弹进入木块的深度为s,相互作用时间为t,若木块对子弹的相互作用力为F视为恒定,则下列关系中正确的是( )
如图所示,质量为M的木块放在光滑的水平面上,质量为m的子弹以速度v0沿水平方向射中木块,并最终留在木块中与木块一起以速度v运动.已知当子弹相对木块静止时,木块前进距离为L,子弹进入木块的深度为s,相互作用时间为t,若木块对子弹的相互作用力为F视为恒定,则下列关系中正确的是( )| A. | FL=$\frac{1}{2}$mv02 | B. | Ft=Mv | ||
| C. | Fs=$\frac{1}{2}$mv02-$\frac{1}{2}$(M+m)v2 | D. | Ft=mv0-(M+m)v |
 如图所示,光滑水平面上,一物块受到恒定拉力F的作用,F与水平方向的夹角为θ.拉力F在水平方向的分力大小等于Fcosθ.物块在拉力F的作用下由静止开始沿水平面运动的位移为s 的过程中,物体动能的增加量等于Fscosθ.
如图所示,光滑水平面上,一物块受到恒定拉力F的作用,F与水平方向的夹角为θ.拉力F在水平方向的分力大小等于Fcosθ.物块在拉力F的作用下由静止开始沿水平面运动的位移为s 的过程中,物体动能的增加量等于Fscosθ. 如图所示,在光滑水平面上有一个正三角形的闭合金属线圈,它恰好处于具有直线边界的匀强磁场外面,三角形的底边与磁场边界平行,磁场的磁感应强度方向垂直纸面向里,如果使线圈以垂直于磁场边界的速度匀速进入磁场,则图中线圈受到的外力或线圈中的感应电流与移动距离的关系可能正确的是( )
如图所示,在光滑水平面上有一个正三角形的闭合金属线圈,它恰好处于具有直线边界的匀强磁场外面,三角形的底边与磁场边界平行,磁场的磁感应强度方向垂直纸面向里,如果使线圈以垂直于磁场边界的速度匀速进入磁场,则图中线圈受到的外力或线圈中的感应电流与移动距离的关系可能正确的是( )


