��Ŀ����
6��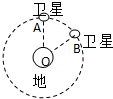 ��2010����������Ŀ�������У��ҹ��������Ƶġ�����һ�š����ǵ���ϵͳ�����˾����ã���ϵͳ���е�������λ�ȹ��ܣ���������ϵͳ��������������ȵĹ���������ͬһ����Ƶ���O������Բ���˶�������뾶Ϊr��ijʱ�������Ƿֱ�λ�ڹ���ϵ�A��B��λ�ã���ͼ��ʾ����������˳ʱ�뷽�����У����������������ٶ�Ϊg������뾶ΪR����AOB=60�㣬�������ж���ȷ���ǣ�������
��2010����������Ŀ�������У��ҹ��������Ƶġ�����һ�š����ǵ���ϵͳ�����˾����ã���ϵͳ���е�������λ�ȹ��ܣ���������ϵͳ��������������ȵĹ���������ͬһ����Ƶ���O������Բ���˶�������뾶Ϊr��ijʱ�������Ƿֱ�λ�ڹ���ϵ�A��B��λ�ã���ͼ��ʾ����������˳ʱ�뷽�����У����������������ٶ�Ϊg������뾶ΪR����AOB=60�㣬�������ж���ȷ���ǣ�������| A�� | ����������ǣ�����ٶ�Ҳ�� | |
| B�� | ����1���������һ����������2 | |
| C�� | ����1��λ��A�˶���λ��B����ʱ��Ϊ$\frac{��r}{3R}\sqrt{\frac{r}{R}}$ | |
| D�� | ����1��λ��A�˶���λ��B�Ĺ�����������������Ϊ�� |
���� ������Բ���˶��������������ṩ����������ʽ�õ����ٶȺ����ڵı���ʽ���������ٶȵĹ�ϵ�����˶�ѧ��ʽ�������1��λ��A�˶���λ��B�����ʱ�䣻������������������û��λ��ʱ������������
��� �⣺A����$G\frac{Mm}{{r}_{\;}^{2}}=ma$����֪$a=\frac{GM}{{r}_{\;}^{2}}$�������ǵ������أ������ǵļ��ٶȴ�С��ȣ���A����
B������1�������ʱ��Ҫ���٣�����Ҫ�����������������������䣬���ǽ��������˶�������뾶��������������2����B����
C����$T=\sqrt{\frac{4{��}_{\;}^{2}{r}_{\;}^{3}}{GM}}$����$G\frac{Mm}{{R}_{\;}^{2}}=mg$�ɵ�$T=\frac{2��r}{R}\sqrt{\frac{r}{g}}$������1��A��B����ʱ��$t=\frac{T}{6}=\frac{��r}{3R}\sqrt{\frac{r}{g}}$����C����
D���������ܵ��������������ٶȴ�ֱ��������������������D��ȷ��
��ѡ��D
���� �������Ĺؼ��������������ṩ���������Լ����������������������������������ɺ�Բ���˶��Ĺ��ɽ����ʽ������

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
17�� ��ͼ��ʾ����ֱ�ᵯ���¶˹̶���ˮƽ�����ϣ�һС����ᵯ�����Ϸ�ijһ�߶ȴ��������£���������ѹ����ֱ��С����ٶȼ�Ϊ�㣮����С����ᵯ�ɵ�ϵͳ����С��ʼ�뵯�ɽӴ���С���ٶȱ�Ϊ��Ĺ����У��У�������
��ͼ��ʾ����ֱ�ᵯ���¶˹̶���ˮƽ�����ϣ�һС����ᵯ�����Ϸ�ijһ�߶ȴ��������£���������ѹ����ֱ��С����ٶȼ�Ϊ�㣮����С����ᵯ�ɵ�ϵͳ����С��ʼ�뵯�ɽӴ���С���ٶȱ�Ϊ��Ĺ����У��У�������
 ��ͼ��ʾ����ֱ�ᵯ���¶˹̶���ˮƽ�����ϣ�һС����ᵯ�����Ϸ�ijһ�߶ȴ��������£���������ѹ����ֱ��С����ٶȼ�Ϊ�㣮����С����ᵯ�ɵ�ϵͳ����С��ʼ�뵯�ɽӴ���С���ٶȱ�Ϊ��Ĺ����У��У�������
��ͼ��ʾ����ֱ�ᵯ���¶˹̶���ˮƽ�����ϣ�һС����ᵯ�����Ϸ�ijһ�߶ȴ��������£���������ѹ����ֱ��С����ٶȼ�Ϊ�㣮����С����ᵯ�ɵ�ϵͳ����С��ʼ�뵯�ɽӴ���С���ٶȱ�Ϊ��Ĺ����У��У�������| A�� | С��Ķ�������������֮��Խ��ԽС��С��Ķ����뵯������֮��Խ��ԽС | |
| B�� | С��Ķ�������������֮��Խ��ԽС��С��Ķ����뵯������֮��Խ��Խ�� | |
| C�� | С��Ķ�������������֮��Խ��Խ��С��Ķ����뵯������֮��Խ��Խ�� | |
| D�� | С��Ķ�������������֮��Խ��Խ��С��Ķ����뵯������֮��Խ��ԽС |
1�����϶���š�̽��������2010��10��1��18ʱ59���������������ķ������գ��ص���ת�ƹ��ֱ������6���ھ��������100km�Ľ��µ�P������һ�Ρ�ɲ���ƶ�������������Բ���I���·��У���μ���ֻ��һ�λ��ᣬ�����ɲ�������Ȳ��������ǻ�ɳ������������Χ���������Ӷ����ܻ��������˶������ɲ�����ȹ������ǾͿ���ײ����������ͬ���������룮֮��������P���־������Ρ�ɲ���ƶ���������ھ��������100km��Բ�ι������������������Բ���˶������������̵��˶��켣��ͼ��ʾ������˵������ȷ���ǣ�������


| A�� | ʵʩ��һ�Ρ�ɲ�����Ĺ��̣���ʹ���϶���š���ʧ�Ķ���ת��Ϊ���ܣ�ת�������л�е���غ� | |
| B�� | ��һ�Ρ�ɲ���ƶ���������ܼ��ٵ�һ���̶ȣ������������������������ | |
| C�� | ��Ρ�ɲ�������������ڹ�������˶������ڱ��ڹ��I�ϳ� | |
| D�� | �����ڹ�������˶���P��ʱ�ļ��ٶ�С���ع��I�˶���P��ʱ�ļ��ٶ� |
15�����ڹ�������˵������ȷ���ǣ�������
| A�� | ����ʸ�� | B�� | ���DZ��� | ||
| C�� | ��Խ������Խ�� | D�� | λ��Խ������Խ�� |
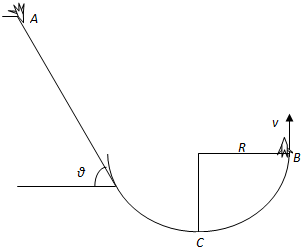 С���������ͼ��ʾ����б��Ͳ���Բ���⻬������ɵĹ������������б�����Ϊ�ȣ���Ϊl��Բ���뾶ΪR��һ����Ϊm�Ļ����A���ɾ�ֹ��б���»�����Բ��ת�����B����ֱ������ɣ���������������F�㶨����ʼ���������з���һ�£������б����Ħ��ϵ��Ϊ�̣�Բ���⻬�����ƿ����������һ�������й������������ֲ��䣬�������ٶ�Ϊg������
С���������ͼ��ʾ����б��Ͳ���Բ���⻬������ɵĹ������������б�����Ϊ�ȣ���Ϊl��Բ���뾶ΪR��һ����Ϊm�Ļ����A���ɾ�ֹ��б���»�����Բ��ת�����B����ֱ������ɣ���������������F�㶨����ʼ���������з���һ�£������б����Ħ��ϵ��Ϊ�̣�Բ���⻬�����ƿ����������һ�������й������������ֲ��䣬�������ٶ�Ϊg������