题目内容
11. 在做“用单摆测定重力加速度”的实验时,用摆长l和周期T计算重力加速度的公式是g=$\frac{4{π}^{2}l}{{T}^{2}}$,如果已知摆球的直径为2.00cm,摆线长度为99.00cm,那么摆长是100.00cm,如果测定了50次全振动的时间如图中秒表所示,那么秒表读数是99.7s,单摆周期是1.994s.
在做“用单摆测定重力加速度”的实验时,用摆长l和周期T计算重力加速度的公式是g=$\frac{4{π}^{2}l}{{T}^{2}}$,如果已知摆球的直径为2.00cm,摆线长度为99.00cm,那么摆长是100.00cm,如果测定了50次全振动的时间如图中秒表所示,那么秒表读数是99.7s,单摆周期是1.994s. (1)现有如下测量工具:A.时钟;B.秒表; C.天平;D.毫米刻度尺.本实验所需的测量工具有BD;
(2)如果某同学用此装置测出的重力加速度的结果比当地重力加速度的真实值偏大,他在实验操作上可能出现的失误是C
A.测量摆长时没有加上摆球半径
B.选用摆球的质量偏大
C.在时间t内的n次全振动误记为n+1次
D.在时间t内的n次全振动误记为n-1次.
(3)为了提高实验精度,在实验中可改变几次摆长l并测出相应的周期T,从而得出一组对应的l和T的数值,再以l为纵坐标、T2为横坐标将所得数据连成直线,并求得该直线的斜率K.则重力加速度g=4π2k.(用K表示)
分析 根据单摆的周期公式T=2π列式求解重力加速度;摆长等于线长加上球的半径;周期T=2π$\sqrt{\frac{l}{g}}$=$\frac{t}{n}$;
(1)根据实验的原理选择合适的测量工具;
(2)根据测量重力加速度的表达式分析即可;
(3)由单摆周期表达式可得T2与L的关系式,得到斜率k的表达式,进而可求得g值.
解答 解:根据单摆的周期公式T=2π$\sqrt{\frac{l}{g}}$,解得:g=$\frac{4{π}^{2}l}{{T}^{2}}$;
摆长:l=99.00cm-$\frac{2}{2}$cm=100.00cm;
分钟读数为1.5min,秒针读数为9.7s,故秒表读数:99.7s;
周期:T=$\frac{t}{n}=\frac{99.7}{50}=1.994$s
(1)由于摆长l=L+$\frac{d}{2}$,g=$\frac{4{π}^{2}l}{{T}^{2}}$,所以需要测量的物理量为时间、线的长度和摆球的直径,所以需要的测量工具是秒表和毫米刻度尺.
故选:BD;
(2)根据g=$\frac{4{π}^{2}l}{{T}^{2}}$,
A、测量摆长时没有加上摆球半径,则摆长的测量值偏小,则重力加速度的测量值偏小.故A错误;
B、根据公式可知,摆球的质量对测量的结果没有影响.故B错误;
C、在时间t内的n次全振动误记为n+1次,则周期测量值偏小,重力加速度测量值偏大.故C正确;
D、在时间t内的n次全振动误记为n-1次,则周期测量值偏大,重力加速度测量值偏小.故D错误.
故选:C
(3)由单摆周期表达式T=2π$\sqrt{\frac{L}{g}}$可得:T2=$\frac{4{π}^{2}L}{g}$
故以l为横坐标、T2为纵坐标得到的图象的斜率为:k=$\frac{L}{{T}^{2}}=\frac{g}{4{π}^{2}}$
解得:g=4π2k
故答案为:$\frac{4{π}^{2}l}{{T}^{2}}$,100.00cm,99.7,1.994;(1)BD;(2)D;(3)4π2k
点评 解决本题的关键掌握游标卡尺的读数方法,以及掌握单摆的周期公式,会通过重力加速度的表达式分析误差引起的原因.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案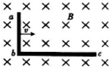 如图所示,水平桌面上放置电阻不计、长度分别为l1、l2(l2>l1)的直金属棒ab和bc连接而成的直角金属架,金属架处于磁感应强度大小为B、方向竖直向下的匀强磁场中.当金属架以速率v沿着bc方向匀速移动时,直角金属架两端的电压为( )
如图所示,水平桌面上放置电阻不计、长度分别为l1、l2(l2>l1)的直金属棒ab和bc连接而成的直角金属架,金属架处于磁感应强度大小为B、方向竖直向下的匀强磁场中.当金属架以速率v沿着bc方向匀速移动时,直角金属架两端的电压为( )| A. | Bl1v | B. | Bl2v | C. | B(l1+l2)v | D. | B(l2-l1)v |
| A. | $\frac{R′}{R}$g0 | B. | $\frac{ρ′}{ρ}$g0 | C. | $\frac{R′ρ′}{Rρ}$g0 | D. | $\frac{Rρ}{R′ρ′}$g0 |
| A. | 若摆长变为原来的$\frac{1}{4}$,则周期变为1s | |
| B. | 若摆球的质量减为原来的$\frac{1}{4}$,则周期变为1s | |
| C. | 若振幅减为原来的$\frac{1}{4}$,则周期变为1s | |
| D. | 若重力加速度减为原来的$\frac{1}{4}$,则周期不变 |

| A. | 交变电流的频率 f=0.2 Hz | |
| B. | 交变电流的有效值I=20$\sqrt{2}$A | |
| C. | 交变电流瞬时值表达式 i=20sin0.02t A | |
| D. | 在t=$\frac{T}{8}$时刻,电流的大小与其有效值相等 |
| A. | 可以计算神舟六号飞船绕地球的太空飞行离地球表面的高度h | |
| B. | 可以计算神舟六号飞船在绕地球的太空飞行的加速度 | |
| C. | 飞船返回舱打开减速伞下降的过程中,飞船中的宇航员处于失重状态 | |
| D. | 神舟六号飞船绕地球的太空飞行速度比月球绕地球运行的速度要小 |
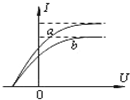 用同一光电管研究a、b两种单色光产生的光电效应,得到光电流I与光电管两极间所加电压U的关系如图.则这两种光( )
用同一光电管研究a、b两种单色光产生的光电效应,得到光电流I与光电管两极间所加电压U的关系如图.则这两种光( )| A. | 两种光在光电管内的波长关系为λa>λb | |
| B. | 照射该光电管时a光使其逸出的光电子最大初动能大 | |
| C. | 实验中a的光的强度大于b光 | |
| D. | a光光子能量大于b光光子能量 |

