题目内容
7. 如图所示,在水平桌面的边角处有一轻质光滑的定滑轮K,一条不可伸长的轻绳绕过K分别与物块A、B相连,A、B的质量分别为mA、mB,开始时系统处于静止状态.现用一水平恒力F拉物块A,使物块B上升.已知当B上升距离为h时,B的速度为v.求:
如图所示,在水平桌面的边角处有一轻质光滑的定滑轮K,一条不可伸长的轻绳绕过K分别与物块A、B相连,A、B的质量分别为mA、mB,开始时系统处于静止状态.现用一水平恒力F拉物块A,使物块B上升.已知当B上升距离为h时,B的速度为v.求:(1)此过程中物块A克服摩擦力所做的功(重力加速度为g);
(2)轻绳对物块B做的功;
(3)系统机械能的变化量及机械能是增加还是减少?
分析 (1)AB组在一个整体,故AB的速度一定相同,则动能定理可求得A克服摩擦力所做的功;
(2)对B,根据动能定理列式求解;
(3))对AB组成的系统,由于摩擦力对系统做负功,所以系统机械能减少,减少量等于克服摩擦力做的功.
解答 解:(1)由于连接AB绳子在运动过程中未松,故AB有一样的速度大小,对AB系统,由动能定理有:
Fh-W-mBgh=$\frac{1}{2}$(mA+mB)v2
求得:W=Fh-mBgh-$\frac{1}{2}$(mA+mB)v2;
(2)对B,根据动能定理得:
$\frac{1}{2}{m}_{B}{v}^{2}=W′-{m}_{B}gh$
解得:W′=$\frac{1}{2}{m}_{B}{v}^{2}-{m}_{B}gh$
(3)对AB组成的系统,由于摩擦力对系统做负功,所以系统机械能减少,减少量△E=Fh-mBgh-$\frac{1}{2}$(mA+mB)v2.
答:(1)A克服摩擦力所做的功为Fh-mBgh-$\frac{1}{2}$(mA+mB)v2;
(2)轻绳对物块B做的功为$\frac{1}{2}{m}_{B}{v}^{2}-{m}_{B}gh$;
(3)系统机械能的变化量为Fh-mBgh-$\frac{1}{2}$(mA+mB)v2,机械能减少.
点评 本题考查动能定理的应用,解题时应将B作为整体分析,不必考虑AB间的相互作用力做功,难度适中.

练习册系列答案
相关题目
17.科学家利用核反应获取氧,再利用氘和氚的核反应获得能量.核反应方程式为X+Y→$\left.\begin{array}{l}{4}\\{2}\end{array}\right.$He+$\left.\begin{array}{l}{3}\\{1}\end{array}\right.$H+4.9MeV和$\left.\begin{array}{l}{2}\\{1}\end{array}\right.$H+$\left.\begin{array}{l}{3}\\{1}\end{array}\right.$H→$\left.\begin{array}{l}{4}\\{2}\end{array}\right.$He+X+17.6MeV.下列表述正确的是( )
| A. | X是中子 | B. | Y的质子数为3,中子数为6 | ||
| C. | 两个核反应都没有质量亏损 | D. | 两个核反应都有质量亏损 | ||
| E. | 氘和氚的核反应是核聚变反应 |
18.将一个物块以一定的初速度从地面上某一高度水平抛出,不计空气阻力,取水平地面为零势能面,已知该物块在抛出点的动能是其重力势能的两倍.则该物块落地时的速度与水平方向的夹角的正切值为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
15.物理学和计算机技术的发展推动了医学影像诊断技术的进步.
彩色超声波检测仪,简称彩超,工作时向人体发射频率已知的超声波,当超声波遇到流向远离探头的血流时探头接收的回波信号频率会降低,当超声波遇到流向靠近探头的血流时探头接收的回波信号频率会升高.利用计算机技术给这些信号加上色彩,显示在屏幕上,可以帮助医生判定血流的方向、流速的大小和性质.
计算机辅助X射线断层摄影,简称T.工作时X射线束对人体的某一部分按一定厚度的层面进行扫描,部分射线穿透人体被检测器接收.由于人体各种组织的疏密程度不同,检测器接收到的射线就有了差异,从而可以帮助医生诊断病变.
根据以上信息,可以判断下列说法中正确的是( )
彩色超声波检测仪,简称彩超,工作时向人体发射频率已知的超声波,当超声波遇到流向远离探头的血流时探头接收的回波信号频率会降低,当超声波遇到流向靠近探头的血流时探头接收的回波信号频率会升高.利用计算机技术给这些信号加上色彩,显示在屏幕上,可以帮助医生判定血流的方向、流速的大小和性质.
计算机辅助X射线断层摄影,简称T.工作时X射线束对人体的某一部分按一定厚度的层面进行扫描,部分射线穿透人体被检测器接收.由于人体各种组织的疏密程度不同,检测器接收到的射线就有了差异,从而可以帮助医生诊断病变.
根据以上信息,可以判断下列说法中正确的是( )
| A. | 彩超工作时利用了多普勒效应 | |
| B. | CT工作时利用了波的衍射现象 | |
| C. | 彩超和CT工作时间向人体发射的波都是纵波 | |
| D. | 彩超和CT工作时间向人体发射的波都是电磁波 |
2. 如图所示,一根跨过光滑定滑轮的轻绳,两端各有一杂技演员.a站在地面上,b从图示位置由静止开始向下摆动,运动过程中绳始终处于伸直状态,当演员b摆至最低点时,a刚好对地面无压力,则下列说法正确的是( )
如图所示,一根跨过光滑定滑轮的轻绳,两端各有一杂技演员.a站在地面上,b从图示位置由静止开始向下摆动,运动过程中绳始终处于伸直状态,当演员b摆至最低点时,a刚好对地面无压力,则下列说法正确的是( )
 如图所示,一根跨过光滑定滑轮的轻绳,两端各有一杂技演员.a站在地面上,b从图示位置由静止开始向下摆动,运动过程中绳始终处于伸直状态,当演员b摆至最低点时,a刚好对地面无压力,则下列说法正确的是( )
如图所示,一根跨过光滑定滑轮的轻绳,两端各有一杂技演员.a站在地面上,b从图示位置由静止开始向下摆动,运动过程中绳始终处于伸直状态,当演员b摆至最低点时,a刚好对地面无压力,则下列说法正确的是( )| A. | a、b两演员的质量相等 | |
| B. | b演员运动过程中机械能守恒 | |
| C. | b演员从图示位置运动到最低点的过程中受到绳子的拉力一直增大 | |
| D. | b演员从图示位置运动到最低点的过程中所受到的合力的功率一直增大 |
12. 如图所示,一个质量为m的足球被以v0速度由地面踢起,当它到达离地面高度为h的B点时如取B点为零重力势能参考平面,下列说法中正确的是( )
如图所示,一个质量为m的足球被以v0速度由地面踢起,当它到达离地面高度为h的B点时如取B点为零重力势能参考平面,下列说法中正确的是( )
 如图所示,一个质量为m的足球被以v0速度由地面踢起,当它到达离地面高度为h的B点时如取B点为零重力势能参考平面,下列说法中正确的是( )
如图所示,一个质量为m的足球被以v0速度由地面踢起,当它到达离地面高度为h的B点时如取B点为零重力势能参考平面,下列说法中正确的是( )| A. | 在B点处的重力势能为mgh | B. | 在B点处的机械能为$\frac{1}{2}$mv02-mgh | ||
| C. | 在B点处的机械能为$\frac{1}{2}$mv02+mgh | D. | 在B点处的动能为$\frac{1}{2}$mv02-mgh |
17. 如图所示,在一次空地对抗军事演习中,离地H高处的飞机以水平速度υ1发射一颗炮弹,欲轰炸地面目标P,反应灵敏的地面拦截系统同时以速度υ2竖直向上发射炸弹拦截.不计空气阻力,不计炮弹的长度.若拦截成功,则( )
如图所示,在一次空地对抗军事演习中,离地H高处的飞机以水平速度υ1发射一颗炮弹,欲轰炸地面目标P,反应灵敏的地面拦截系统同时以速度υ2竖直向上发射炸弹拦截.不计空气阻力,不计炮弹的长度.若拦截成功,则( )
 如图所示,在一次空地对抗军事演习中,离地H高处的飞机以水平速度υ1发射一颗炮弹,欲轰炸地面目标P,反应灵敏的地面拦截系统同时以速度υ2竖直向上发射炸弹拦截.不计空气阻力,不计炮弹的长度.若拦截成功,则( )
如图所示,在一次空地对抗军事演习中,离地H高处的飞机以水平速度υ1发射一颗炮弹,欲轰炸地面目标P,反应灵敏的地面拦截系统同时以速度υ2竖直向上发射炸弹拦截.不计空气阻力,不计炮弹的长度.若拦截成功,则( )| A. | 拦截炮弹运行的时间为$\frac{H}{{v}_{1}}$ | |
| B. | 拦截炮弹运行的时间为$\frac{H}{{v}_{2}}$ | |
| C. | 拦截系统距飞机的水平距离为$\frac{H{v}_{1}}{{v}_{2}}$ | |
| D. | 拦截系统距飞机的水平距离为$\frac{H{v}_{2}}{{v}_{1}}$ |
18.下列说法不符合物理学史的是( )
| A. | 奥斯特发现了电流的磁效应 | |
| B. | 牛顿解释了涡旋电场的产生原理 | |
| C. | 法拉第发现了电磁感应现象 | |
| D. | 楞次找到了判断感应电流方向的方法 |
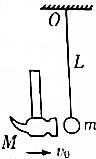 如图所示,如果悬挂球的绳子能承受的最大拉力F=10N,球的质量m=0.5kg,L=0.3m,锤头的质量M=0.866kg,如果锤沿水平方向击打球m,试求锤头的速度多大时才能把绳打断.(设m原来是静止的,打击后锤头是静止的,取g=10m/s2)
如图所示,如果悬挂球的绳子能承受的最大拉力F=10N,球的质量m=0.5kg,L=0.3m,锤头的质量M=0.866kg,如果锤沿水平方向击打球m,试求锤头的速度多大时才能把绳打断.(设m原来是静止的,打击后锤头是静止的,取g=10m/s2)