题目内容
13. 如图所示,在y轴右侧加有垂直纸面向外的匀强磁场,磁感强度B=1T.从原点o处向第I象限发射一比荷$\frac{q}{m}$=1×104C的带电粒子(重力不计),速度大小υ0=103m/s,方向垂直于磁场且与x轴正方向成θ=30°角进入磁场,粒子经过x轴后再从y轴上的Q点离开磁场,试问:
如图所示,在y轴右侧加有垂直纸面向外的匀强磁场,磁感强度B=1T.从原点o处向第I象限发射一比荷$\frac{q}{m}$=1×104C的带电粒子(重力不计),速度大小υ0=103m/s,方向垂直于磁场且与x轴正方向成θ=30°角进入磁场,粒子经过x轴后再从y轴上的Q点离开磁场,试问:(1)粒子带什么电;
(2)求OQ的距离;
(3)求粒子在该磁场中运动的时间.
分析 (1)根据粒子运动方向,应用左手定则判断粒子的电性.
(2)粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律求出粒子的轨道半径,然后求出OQ的距离.
(3)根据粒子转过的圆心角与粒子做圆周运动的轨道半径,求出粒子的运动时间.
解答 解:(1)由题意可知粒子进入磁场后向下偏转,刚进入磁场时所受洛伦兹力垂直与速度方向斜向右下方,由左手定则可知,粒子带正 电.
电.
(2)粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律得:qυ0B=m$\frac{{v}_{0}^{2}}{r}$,代入数据解得:r=0.1m,
粒子运动轨迹如图所示,由几何知识得:α=120°,OQ=2rsin$\frac{α}{2}$=0.1$\sqrt{3}$m≈0.1732m;
(3)粒子在磁场中做圆周运动的周期:T=$\frac{2πm}{qB}$=2π×10-4s,
粒子在磁场中的运动时间:t=$\frac{360°-α}{360°}$T=$\frac{4π}{3}$×10-4s;
答:(1)粒子带正电;
(2)OQ的距离为0.1732m;
(3)粒子在该磁场中运动的时间为$\frac{4π}{3}$×10-4s.
点评 本题考查带电粒子在匀强磁场中的运动,洛伦兹力提供向心力是基础,正确画出粒子运动的轨迹是解决问题的关键.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
3.质量为2t的汽车,发动机的额定功率为80kW,在阻力不变的水平公路上,以额定功率启动,其最大速度为20m/s,当汽车的速度为16m/s时的加速度大小为( )
| A. | 0.5m/s2 | B. | 1m/s2 | C. | 1.5m/s2 | D. | 2m/s2 |
1.2010的诺贝尔物理学奖授予英国曼彻斯特大学科学家安德烈.海姆和康斯坦丁.诺沃肖洛夫,以表彰他们对石墨烯的研究.他们最初是用透明脐带从石墨晶体上“粘”出一片石墨烯的.我们平常所用的2B铅笔中就含有石墨,能够导电.某同学设计了探究2B铅笔芯伏特曲线的实验.现有以下仪器
A、电流表:量程为0~3A,内阻约为1ΩB、电压表:量程为0~5V,内阻约为1.5KΩ
C、电压表:量程为0~2V,内阻约为1KΩD、滑动变阻器:阻值范围为0~10Ω,额定电流2A
E、蓄电池:总电势为6V,内阻较小 F、蓄电池:总电动势为3V,内阻较小
G、导线若干,和一个电键.
(1)一同学设计了如力图1中的a、b两种电路,为使测量尽量准确,要求进行多次测量,你认为应该选择a电路图:电源选用E,电压表选用B.(填序号)
(2)选择能够尽量准确减少误差的电路图连线进行实验,所得各组数据如下表
①根据实验数据在图2中画出I-U图线
②由图线得出待测2B铅笔阻值为2.5Ω,其待测2B铅笔芯的测量值比真实值偏小(选填:“大”或“小”)

A、电流表:量程为0~3A,内阻约为1ΩB、电压表:量程为0~5V,内阻约为1.5KΩ
C、电压表:量程为0~2V,内阻约为1KΩD、滑动变阻器:阻值范围为0~10Ω,额定电流2A
E、蓄电池:总电势为6V,内阻较小 F、蓄电池:总电动势为3V,内阻较小
G、导线若干,和一个电键.
(1)一同学设计了如力图1中的a、b两种电路,为使测量尽量准确,要求进行多次测量,你认为应该选择a电路图:电源选用E,电压表选用B.(填序号)
(2)选择能够尽量准确减少误差的电路图连线进行实验,所得各组数据如下表
| 次数 | 1 | 2 | 3 | 4 | 5 | 6 |
| U/V | 0.5 | 1.0 | 1.5 | 2.0 | 2.4 | 3.1 |
| I/A | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 |
②由图线得出待测2B铅笔阻值为2.5Ω,其待测2B铅笔芯的测量值比真实值偏小(选填:“大”或“小”)

8. 汤姆逊通过对阴极射线的研究发现了电子,如图所示,阴极射线管的两极分别接在直流高压电源两端,把电子射线管放在蹄形磁铁的两极之间,可以观察荧光屏上的电子运动的轨迹偏转方向是( )
汤姆逊通过对阴极射线的研究发现了电子,如图所示,阴极射线管的两极分别接在直流高压电源两端,把电子射线管放在蹄形磁铁的两极之间,可以观察荧光屏上的电子运动的轨迹偏转方向是( )
 汤姆逊通过对阴极射线的研究发现了电子,如图所示,阴极射线管的两极分别接在直流高压电源两端,把电子射线管放在蹄形磁铁的两极之间,可以观察荧光屏上的电子运动的轨迹偏转方向是( )
汤姆逊通过对阴极射线的研究发现了电子,如图所示,阴极射线管的两极分别接在直流高压电源两端,把电子射线管放在蹄形磁铁的两极之间,可以观察荧光屏上的电子运动的轨迹偏转方向是( )| A. | 向左 | B. | 向右 | C. | 向上 | D. | 向下 |
18.如图1所示的黑箱中有三只完全相同的电学子元件,小明使用多用电表对其进行探测.

(1)在使用多用电表前,发现指针不在左边的“0”刻度线处,应先调整图2中多用电表的A(选填“A”、“B”或“C”)
(2)在判定黑箱中无电源后,将选择开关旋至“×1”挡,调节好多用电表,测量各接点间阻值,测量中发现,每对接点间正反方向阻值均相等,测量记录如表,两表笔分别接a、b时,多用电表的示数如图2所示.请将读数填入表.
(3)设计黑箱中的电路,在图3的方框内画出一种可能的电路.

(1)在使用多用电表前,发现指针不在左边的“0”刻度线处,应先调整图2中多用电表的A(选填“A”、“B”或“C”)
(2)在判定黑箱中无电源后,将选择开关旋至“×1”挡,调节好多用电表,测量各接点间阻值,测量中发现,每对接点间正反方向阻值均相等,测量记录如表,两表笔分别接a、b时,多用电表的示数如图2所示.请将读数填入表.
| 两表笔接的接点 | 多用电表的示数 |
| a、b | 5Ω |
| a、c | 10.0Ω |
| b、c | 15.0Ω |
5. 一列简谐横波沿x轴正方向传播,在t1=0时,波传播到x轴上的质点B,在它左边的质点A恰好位于负最大位移处,如图所示.在t2=0.6s时,质点A恰好第二次出现在正的最大位移处,则( )
一列简谐横波沿x轴正方向传播,在t1=0时,波传播到x轴上的质点B,在它左边的质点A恰好位于负最大位移处,如图所示.在t2=0.6s时,质点A恰好第二次出现在正的最大位移处,则( )
 一列简谐横波沿x轴正方向传播,在t1=0时,波传播到x轴上的质点B,在它左边的质点A恰好位于负最大位移处,如图所示.在t2=0.6s时,质点A恰好第二次出现在正的最大位移处,则( )
一列简谐横波沿x轴正方向传播,在t1=0时,波传播到x轴上的质点B,在它左边的质点A恰好位于负最大位移处,如图所示.在t2=0.6s时,质点A恰好第二次出现在正的最大位移处,则( )| A. | 该简谐波的波速等于5m/s | |
| B. | t2=0.6s时,质点C在平衡位置处且向下运动 | |
| C. | t2=0.6s时,质点C在平衡位置处且向上运动 | |
| D. | 当质点D第一次出现在正向最大位移处时,质点B恰好在平衡位置且向下运动 |
10.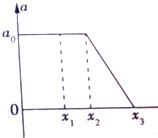 放在水平面上的物体,在力F作用下开始运动,以物体静止时的位置为坐标原点,力F的方向为正方向建立x轴,物体的加速度随位移的变化图象如图所示.下列说法中错误的是( )
放在水平面上的物体,在力F作用下开始运动,以物体静止时的位置为坐标原点,力F的方向为正方向建立x轴,物体的加速度随位移的变化图象如图所示.下列说法中错误的是( )
 放在水平面上的物体,在力F作用下开始运动,以物体静止时的位置为坐标原点,力F的方向为正方向建立x轴,物体的加速度随位移的变化图象如图所示.下列说法中错误的是( )
放在水平面上的物体,在力F作用下开始运动,以物体静止时的位置为坐标原点,力F的方向为正方向建立x轴,物体的加速度随位移的变化图象如图所示.下列说法中错误的是( )| A. | 0~x2过程中物体做匀加速直线运动,x2~x3过程中物体做匀减速运动 | |
| B. | 位移为x1时,物体的速度大小为$\sqrt{2{a}_{0}{x}_{1}}$ | |
| C. | 位移为x2时,物体的速度达到最大 | |
| D. | 物体的最大速度为$\sqrt{{a}_{0}({x}_{2+}{x}_{3})}$ |
