��Ŀ����
19����ͼa��ʾ����ǿ�ų���ֱ��xOyƽ�棬�Ÿ�Ӧǿ��B1��ͼb��ʾ���ɱ仯����ֱ��ֽ������Ϊ������t=0ʱ��һ�Ⱥ�Ϊ$\frac{q}{m}$=1��105C/kg�Ĵ��������Ӵ�ԭ����y�����������룬�ٶȴ�Сv=3��104m/s������������������1���������������ǿ�ų����˶��Ĺ���뾶��
��2����t=$\frac{��}{2}$��10-4sʱ�������ӵ����꣮
��3������b�дų����䣬�ټ�һ��ֱ��xOyƽ������ĺ㶨��ǿ�ų�B2����Ÿ�Ӧǿ��Ϊ0.3T����t=0ʱ����������ԭ�����ٶȴ�ԭ�����룬�����ӻص�����ԭ���ʱ�̣�

���� ��1���������������ṩ�������з��̼������������������ǿ�ų����˶��Ĺ���뾶��
��2����������������ڴų����˶������ڣ��ٷֱ������0��$\frac{��}{4}$��10-4s��$\frac{��}{4}$��10-4s��$\frac{��}{2}$��10-4s�����У������˶��˵����ں�Բ����Ӧ��Բ�Ľǣ��������ӵ��˶��켣ͼ�����ü��ι�ϵ����������ӵ����ꣻ
��3������ʩ��B2=0.3T����ǿ�ų���ԭ�ų����Ӻ���ɱ仯ͼ���ֱ������nT��t��nT+$\frac{T}{2}$��nT+$\frac{T}{2}$��t�ܣ�n+1��T��n=0��1��2������ʱ�����˶��˵����ڣ����������˶��켣ͼ����������ӻص�����ԭ���ʱ�̣�
��� �⣺��1��������������ǿ�ų����˶������������ṩ��������
����qvB1=m$\frac{{v}^{2}}{r}$��
�������ݽ�ã�r=$\frac{mv}{q{B}_{1}}$=$\frac{3��1{0}^{4}}{1��1{0}^{5}��0.5}$m=0.6m��
��2�����������ڴų����˶������ڣ�
T0=$\frac{2��m}{{B}_{1}q}$=$\frac{2��}{5}$��10-4s��
��0��$\frac{��}{4}$��10-4s�����У������˶���$\frac{5{T}_{0}}{8}$��
Բ����Ӧ��Բ�Ľǣ���1=$\frac{5��}{4}$��
��$\frac{��}{4}$��10-4s��$\frac{��}{2}$��10-4s�����У��������˶���$\frac{5{T}_{0}}{8}$��
Բ����Ӧ��Բ�Ľǣ���2=$\frac{5��}{4}$��
�켣��ͼa��ʾ�����ݼ��ι�ϵ��֪��
�����꣺x=2r+2rsin$\frac{��}{4}$=$\frac{3}{5}$��2+$\sqrt{2}$��m��
�����꣺y=-2rcos$\frac{��}{4}$=-$\frac{3\sqrt{2}}{5}$m��
�ʴ������ӵ�����Ϊ[$\frac{3}{5}$��2+$\sqrt{2}$��m��-$\frac{3\sqrt{2}}{5}$m]��
��3��ʩ��B2=0.3T����ǿ�ų���ԭ�ų����Ӻ���ͼb��ʾ��
�ٵ�nT��t��nT+$\frac{T}{2}$��n=0��1��2������ʱ��
T1=$\frac{2��m}{q��{B}_{1}+{B}_{2}��}$=$\frac{��}{4}$��10-4s��
�ڵ�nT+$\frac{T}{2}$��t�ܣ�n+1��T��n=0��1��2������ʱ��
T2=$\frac{2��m}{q��{B}_{1}-{B}_{2}��}$=��10-4s��
�����˶��켣��ͼc��ʾ��
�����ӻص�ԭ���ʱ��Ϊ��
t1=��$\frac{��}{4}$+2n����10-4s��
t2=2��n+1����10-4s ��n=0��1��2��������
�𣺣�1���������������ǿ�ų����˶��Ĺ���뾶Ϊ0.6m��
��2��t=$\frac{��}{2}$��10-4sʱ�������ӵ�����Ϊ[$\frac{3}{5}$��2+$\sqrt{2}$��m��-$\frac{3\sqrt{2}}{5}$m]��
��3�����ӻص�����ԭ���ʱ��Ϊt1=��$\frac{��}{4}$+2n�У���10-4s��t2=2��n+1���С�10-4s ��n=0��1��2��������
���� �����Ǵ�����������ǿ�ų��е��˶����⣬����ʱҪ����������ӵ��˶��켣���������ӵ��˶��켣ͼ����ϼ���֪ʶ������⣬ͬʱҪע�������˶��������ԣ����̱Ƚϸ��ӣ����ڿ���ѧ���ۺϷ��������������

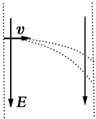 ��ͼ��ʾ��һ���������ٶ�v��ֱ�糡���������н���ǿ�糡�У�������糡����ʱ����λ��Ϊd1������Ļ�ʹ�����Ӵ�ͬһλ����2v�ٶȴ�ֱ�糡�������룬���������н�糡ʱ�IJ���λ��ӦΪ��������
��ͼ��ʾ��һ���������ٶ�v��ֱ�糡���������н���ǿ�糡�У�������糡����ʱ����λ��Ϊd1������Ļ�ʹ�����Ӵ�ͬһλ����2v�ٶȴ�ֱ�糡�������룬���������н�糡ʱ�IJ���λ��ӦΪ��������| A�� | d2=d1 | B�� | d2=$\frac{{d}_{1}}{4}$ | C�� | d2=$\frac{{d}_{1}}{8}$ | D�� | d2=$\frac{{d}_{1}}{16}$ |
 ��ͼ��ʾ���̶���ˮƽ���ϵĹ⻬ƽ�н������죬���ΪL���Ҷ˽�����ֵΪR�ĵ��裬�ռ���ڷ�����ֱ���ϡ��Ÿ�Ӧǿ��ΪB����ǿ�ų�������Ϊm������Ϊr�ĵ����ab��̶��������������ڵ����ϣ���ʼʱ�̣�����ǡ������Ȼ���ȣ��������ˮƽ���ҵij��ٶ�v0���������ʼ�ص��������˶����ڴ˹����У������ʼ���뵼�촹ֱ���������ýӴ�����֪������ĵ���r�붨ֵ����R����ֵ��ȣ����Ƶ�����裬������˵������ȷ���ǣ�������
��ͼ��ʾ���̶���ˮƽ���ϵĹ⻬ƽ�н������죬���ΪL���Ҷ˽�����ֵΪR�ĵ��裬�ռ���ڷ�����ֱ���ϡ��Ÿ�Ӧǿ��ΪB����ǿ�ų�������Ϊm������Ϊr�ĵ����ab��̶��������������ڵ����ϣ���ʼʱ�̣�����ǡ������Ȼ���ȣ��������ˮƽ���ҵij��ٶ�v0���������ʼ�ص��������˶����ڴ˹����У������ʼ���뵼�촹ֱ���������ýӴ�����֪������ĵ���r�붨ֵ����R����ֵ��ȣ����Ƶ�����裬������˵������ȷ���ǣ�������| A�� | �������ʼ�˶��ij�ʼʱ���ܵ��İ��������� | |
| B�� | �������ʼ�˶��ij�ʼʱ�̵�������˵ĵ�ѹU=$\frac{1}{2}$BLv0 | |
| C�� | �������ʼ�˶����ٶȵ�һ��Ϊ��ʱ��ϵͳ�ĵ�������Ep=$\frac{1}{2}$m$v_0^2$ | |
| D�� | �ӵ������ʼ�˶�������λ�õĹ����У�����R�ϲ����Ľ�����Q=$\frac{1}{4}$m$v_0^2$ |
| A�� | ����������ĵ���Ϊ10-5 F | |
| B�� | �������������50 V���Ʋ�ʱ�����ݲ���10 ��F | |
| C�� | ���������û�е��Ʋ�ʱ������Ϊ0 | |
| D�� | ����������ӵĵ��Ʋ�ܵ���50 V |

 ��ͼ��ʾ������ͼ��������ֱ����ĴŸ�Ӧǿ��ΪB=0.25T����ǿ�ų��У��������MNPQ����ܵ�����Բ��ƣ��̶���ˮƽ���ڣ�MN��PQƽ�����㹻����MN��PQ���d=$\frac{{\sqrt{3}}}{4}$m��MP��PQ�нǦ�=60�㣬�⻬���ȵ����EF����ֱ��PQ���������������Դ�ֱ���������ٶ�v=2m/s���������˶���������ڻ���������ʼ�ձ����������ýӴ����ҵ����ÿ�ĵ���Ϊ0.4��������P��˲����Ϊ��ʱ��㣮����
��ͼ��ʾ������ͼ��������ֱ����ĴŸ�Ӧǿ��ΪB=0.25T����ǿ�ų��У��������MNPQ����ܵ�����Բ��ƣ��̶���ˮƽ���ڣ�MN��PQƽ�����㹻����MN��PQ���d=$\frac{{\sqrt{3}}}{4}$m��MP��PQ�нǦ�=60�㣬�⻬���ȵ����EF����ֱ��PQ���������������Դ�ֱ���������ٶ�v=2m/s���������˶���������ڻ���������ʼ�ձ����������ýӴ����ҵ����ÿ�ĵ���Ϊ0.4��������P��˲����Ϊ��ʱ��㣮����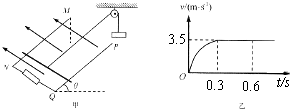 ��ͼ����ʾ��һ�㹻����ֵ���ƵĹ⻬ƽ�н�������MN��PQ֮��ľ���L=0.5m��NQ����������ֵR=2.0���ĵ��裬�Ÿ�Ӧǿ��ΪB����ǿ�ų���ֱ�ڵ�������ƽ�����ϣ�����ƽ����ˮƽ���ļнǦ�=300��һ����m=0.40kg����ֵr=1.0���Ľ�������ֱ�ڵ�����ò��þ�Եϸ��ͨ���⻬�Ķ�����������M=0.80kg������������ϸ�����������ƽ�У��������ص������ϻ��е��ٶ�v��ʱ��t֮��Ĺ�ϵ��ͼ����ʾ����֪��������0��0.3s��ͨ���ĵ�����0.3��0.6s��ͨ��������$\frac{2}{3}$��g=10m/s2����
��ͼ����ʾ��һ�㹻����ֵ���ƵĹ⻬ƽ�н�������MN��PQ֮��ľ���L=0.5m��NQ����������ֵR=2.0���ĵ��裬�Ÿ�Ӧǿ��ΪB����ǿ�ų���ֱ�ڵ�������ƽ�����ϣ�����ƽ����ˮƽ���ļнǦ�=300��һ����m=0.40kg����ֵr=1.0���Ľ�������ֱ�ڵ�����ò��þ�Եϸ��ͨ���⻬�Ķ�����������M=0.80kg������������ϸ�����������ƽ�У��������ص������ϻ��е��ٶ�v��ʱ��t֮��Ĺ�ϵ��ͼ����ʾ����֪��������0��0.3s��ͨ���ĵ�����0.3��0.6s��ͨ��������$\frac{2}{3}$��g=10m/s2���� ��ͼ��ʾ��һ����������Ϊm��������Ϊ+Q���Գ��ٶ�v0��ˮƽ���45�������ռ���ǿ�糡��������ǡ��ֱ���˶���������ǿ�糡��ǿ����СֵΪ$\frac{\sqrt{2}mg}{2q}$��������б�����Ϸ�����ˮƽ�����45�Ƚǣ�
��ͼ��ʾ��һ����������Ϊm��������Ϊ+Q���Գ��ٶ�v0��ˮƽ���45�������ռ���ǿ�糡��������ǡ��ֱ���˶���������ǿ�糡��ǿ����СֵΪ$\frac{\sqrt{2}mg}{2q}$��������б�����Ϸ�����ˮƽ�����45�Ƚǣ� ��ͼ��ʾ����ˮƽ�������ǿ�糡�У�һ������Ϊm ����С���þ�Ե������������������O�㣬ƽ��ʱС��λ��A�㣬��ʱ������ֱ����ļнǦ�=53�㣬����Ϊl��B��C��D��O��ľ����Ϊl��BDˮƽ��OC��ֱ��BO=CO=DO=l��
��ͼ��ʾ����ˮƽ�������ǿ�糡�У�һ������Ϊm ����С���þ�Ե������������������O�㣬ƽ��ʱС��λ��A�㣬��ʱ������ֱ����ļнǦ�=53�㣬����Ϊl��B��C��D��O��ľ����Ϊl��BDˮƽ��OC��ֱ��BO=CO=DO=l��