题目内容
3. 如图所示,光滑水平面上A、B两小球沿同一方向运动,A球的动量4kg•m/s,B球的质量1kg,速度为6m/s,已知两球相碰后,A球的动量减为原来的一半,方向与原方向一致.则( )
如图所示,光滑水平面上A、B两小球沿同一方向运动,A球的动量4kg•m/s,B球的质量1kg,速度为6m/s,已知两球相碰后,A球的动量减为原来的一半,方向与原方向一致.则( )| A. | A球的质量可能为0.4kg | B. | A球的质量可能为0.5kg | ||
| C. | A球碰撞后的速度不可能为4m/s | D. | A球碰撞后的速度不可能为10m/s |
分析 A球能追上B球并与之碰撞,根据动量守恒定律列出等式,根据碰撞后A球不可能运动到B球前方和碰撞过程系统的动能不增加来求解A的质量.并由此分析A的速度范围.
解答 解:AB、由题知,碰撞后A的动量为 p'A=2kg•m/s,根据动量守恒定律有:pA+mBvB=p'A+mBv'B,解得 v'B=8.0m/s.
设A球质量为mA,A球能追上B球并与之碰撞,应满足 vA=$\frac{{p}_{A}}{{m}_{A}}$>vB;碰撞后A球不可能运动到B球前方,故v′A=$\frac{p{′}_{A}}{{m}_{A}}$≤v′B;
碰撞过程系统的总动能不可能增加,故$\frac{{p}_{A}^{2}}{2{m}_{A}}$+$\frac{1}{2}$mBvB2≤$\frac{{p}_{A}^{′2}}{2{m}_{A}}$+$\frac{1}{2}$mBvB′2
解得:$\frac{1}{4}$kg≤mA≤$\frac{3}{7}$kg(或0.25kg≤mA≤0.43kg),所以A球的质量可能为0.4kg,不可能为0.5kg,故A正确,B错误.
CD、碰撞后,B球的速度为v'B=8.0m/s,则A球碰撞后的速度不可能大于8.0m/s,所以A球碰撞后的速度不可能为10m/s.
若A球的质量为0.5kg,则碰撞前A球的速度为8m/s,碰撞后的速度为4m/s,碰撞前后A球动能的减少△EkA=$\frac{{p}_{A}^{2}}{2{m}_{A}}$-$\frac{{p}_{A}^{′2}}{2{m}_{A}}$=$\frac{{4}^{2}}{2×0.5}$-$\frac{{2}^{2}}{2×0.5}$=12J
B球动能的增加量△EkB=$\frac{1}{2}$mBvB′2-$\frac{1}{2}$mBvB2=14J>△EkA,不可能,故CD正确.
故选:ACD
点评 本题的关键要明确碰撞的基本规律:动量守恒定律、碰撞过程中总动能不可能增加,并要符合运动情况,即可正确解题.

| A. | 甲乙两车在这段时间内的位移之比为4:3 | |
| B. | 甲车的功率增大到原来的2倍 | |
| C. | 甲乙两车在这段时间内克服阻力做功之比为12:11 | |
| D. | 甲乙两车在这段时间内牵引力做功之比为3:2 |
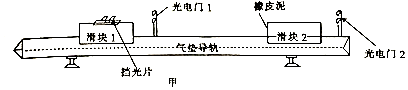
实验过程:
(1)调节气垫导轨水平,并使光电计时器系统正常工作.
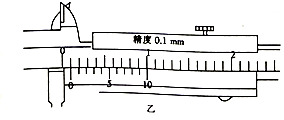
(2)在滑块1上装上挡光片,用游标卡尺测得其挡光宽度L如图乙所示,则L=1.0mm.
(3)在滑块2的碰撞端面粘上橡皮泥(或双面胶纸).
(4)用天平测出滑块1和滑块2的质量m1=0.4kg、m2=0.2kg.
(5)把滑块1和滑块2放在气垫导轨上,让滑块2处于静止状态(v2=0),用滑块1以初速度v1与之碰撞(这时光电计时器系统自动计算时间),撞后两者粘在一起,分别记下滑块1的挡光片碰前通过光电门1的挡光时间t1和碰后通过光电门2的挡光时间t2.
(6)先根据v=$\frac{L}{t}$计算滑块1碰撞前的速度v1及碰后两者的共同速度v;再计算两滑块碰撞前后的动量,并比较两滑块碰撞前后的动量的矢量和.
实验数据:(请在表格中的空白处填上相应的文字或数据)
| 次 数 | 滑块1 | 滑块2 | 碰前系统动量 (kg•m•s-1) | 碰后系统动量 kg•m•s-1 | |||
| v1/(m•s-1) | v/(m•s-1) | v2/(m•s-1) | v/(m•s-1) | m1v1 | m2v2 | (m1+m2)v | |
| 1 | 0.290 | 0.192 | 0 | 0.192 | ① | 0 | 0.115 |
| 2 | 0.453 | 0.296 | 0 | 0.296 | ② | 0 | ③ |
| 结论:④ | |||||||
| A. | 电场强度的方向总是与电场力的方向一致 | |
| B. | 电场强度的大小总是与电场力的大小成正比 | |
| C. | 正电荷受到的电场力的方向与电场强度的方向垂直 | |
| D. | 电场强度是电场的本质属性,与检验电荷无关 |
| A. | 可以从较高轨道上加速追赶 | B. | 可以从较低轨道上加速追赶 | ||
| C. | 只能从同一轨道上加速追赶 | D. | 无论什么轨道上只要加速都行 |
 倾角θ为37°的光滑斜面上固定带轻杆的槽,劲度系数k=20N/m、原长足够长的轻弹簧下端与轻杆相连,开始时杆在槽外的长度l=0.6m,且杆可在槽内移动,杆与槽间的滑动摩擦力大小恒为Ff=6N,杆与槽之间的最大静摩擦力等于滑动摩擦力.质量m=1kg的小车从距弹簧上端l=0.6m处由静止释放沿斜面向下运动.已知弹簧弹性势能为Ep=$\frac{1}{2}$kx2,式中x为弹簧的形变量.在整个运动过程中,弹簧始终处于弹性限度以内.g=10m/s2,sin37°=0.6.下列说法正确的是( )
倾角θ为37°的光滑斜面上固定带轻杆的槽,劲度系数k=20N/m、原长足够长的轻弹簧下端与轻杆相连,开始时杆在槽外的长度l=0.6m,且杆可在槽内移动,杆与槽间的滑动摩擦力大小恒为Ff=6N,杆与槽之间的最大静摩擦力等于滑动摩擦力.质量m=1kg的小车从距弹簧上端l=0.6m处由静止释放沿斜面向下运动.已知弹簧弹性势能为Ep=$\frac{1}{2}$kx2,式中x为弹簧的形变量.在整个运动过程中,弹簧始终处于弹性限度以内.g=10m/s2,sin37°=0.6.下列说法正确的是( )| A. | 在杆完全进入槽内之前,小车先做匀加速运动,然后做加速度逐渐减小的加速运动,最后做匀速直线运动 | |
| B. | 小车从开始运动到杆完全进入槽内所用时间为$\frac{\sqrt{5}}{5}$s | |
| C. | 若杆与槽间的滑动摩擦力大小Ff变为16N,小车、弹簧、轻杆组成的系统机械能一定不守恒 | |
| D. | 若杆与槽间的滑动摩擦力大小Ff变为16N,小车第一次与弹簧作用过程中轻杆移动的距离为0.2m |
 如图所示,在某娱乐比赛项目中,选手通过助跑,趴在手中的塑料盆上,从水平木板的起点线AB开始滑行,过了终点线CD且又不落入水中才算赢,某选手和盆以速度5m/s从起点线位置M出发,恰好能过终点线到达位置N,线AB与CD间距离L=10m,终点线CD离水面的水平距离为d=1.5m,人在盆中相对盆静止不动,人和盆的总质量m=80kg.
如图所示,在某娱乐比赛项目中,选手通过助跑,趴在手中的塑料盆上,从水平木板的起点线AB开始滑行,过了终点线CD且又不落入水中才算赢,某选手和盆以速度5m/s从起点线位置M出发,恰好能过终点线到达位置N,线AB与CD间距离L=10m,终点线CD离水面的水平距离为d=1.5m,人在盆中相对盆静止不动,人和盆的总质量m=80kg.

