题目内容
2. 在以O为圆心,r为半径的圆形空间内,存在垂直干纸面向里的磁场,一带电粒子(不计重力)从A点以速度v0垂直于磁场方向正对圆心O点射入磁场中,从B点射出,已知角AOB=120°,则该带电粒子在磁场中运动时间为( )
在以O为圆心,r为半径的圆形空间内,存在垂直干纸面向里的磁场,一带电粒子(不计重力)从A点以速度v0垂直于磁场方向正对圆心O点射入磁场中,从B点射出,已知角AOB=120°,则该带电粒子在磁场中运动时间为( )| A. | $\frac{2πr}{3{v}_{0}}$ | B. | $\frac{2\sqrt{3}πr}{3{v}_{0}}$ | C. | $\frac{πr}{3{v}_{0}}$ | D. | $\frac{\sqrt{3}πr}{3{v}_{0}}$ |
分析 带电粒子在磁场中做匀速圆周运动,由几何关系可求出圆心角和半径,则可求得粒子转过的弧长,由线速度的定义可求得运动的时间.
解答 解:由图根据几何关系可知,粒子转过的圆心角为60°,R=$\sqrt{3}$r; 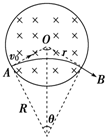
转过的弧长为l=$\frac{60}{360}$×2πR=$\frac{πR}{3}$=$\frac{\sqrt{3}πr}{3}$;
则运动所用时间t=$\frac{l}{{v}_{0}}$=$\frac{\sqrt{3}πr}{3{v}_{0}}$;
故选:D
点评 本题很多同学只想到了用周期来求时间,其实用线速度的定义来求时间也是一个不错的选择,因此在解题中要注意灵活应用数学规律求解.

练习册系列答案
相关题目
7.下列关于动量的说法中正确的是( )
| A. | 质量大的物体动量一定大 | |
| B. | 一个物体的速率改变,它的动量不一定改变 | |
| C. | 只要系统内存在摩擦力,系统的动量就不可能守恒 | |
| D. | 只要系统所受的合外力为零,系统的动量就守恒 |
8.美国的全球卫星定位系统(简称GPS)由24颗卫星组成,卫星分布在等分地球的6个轨道平面上,每个轨道上又分布有4颗卫星,这些卫星距地面的高度均为20000km.我国自行建立的“北斗一号”卫星定位系统由三颗卫星组成,三颗卫星都定位在距地面36000km的地球同步轨道上.比较这些卫星,下列说法中正确的是( )
| A. | “北斗一号”系统中的三颗卫星的质量必须相同,否则它们不能定位在同一轨道上 | |
| B. | GPS的卫星较“北斗一号”的卫星周期更小 | |
| C. | GPS的卫星较“北斗一号”的卫星有更大的加速度 | |
| D. | GPS的卫星较“北斗一号”的卫星有较小的运行速度 |
14. 如图所示,质量为m的小物体静止在半径为R的半球体上,它与半球体间的动摩擦因数为μ,它与球心连线跟水平地面的夹角为θ,则( )
如图所示,质量为m的小物体静止在半径为R的半球体上,它与半球体间的动摩擦因数为μ,它与球心连线跟水平地面的夹角为θ,则( )
 如图所示,质量为m的小物体静止在半径为R的半球体上,它与半球体间的动摩擦因数为μ,它与球心连线跟水平地面的夹角为θ,则( )
如图所示,质量为m的小物体静止在半径为R的半球体上,它与半球体间的动摩擦因数为μ,它与球心连线跟水平地面的夹角为θ,则( )| A. | 地面对半球体的摩擦力方向水平向左 | |
| B. | 小物体所受摩擦力大小mgcosθ | |
| C. | 小物体所受摩擦力大小μmgsinθ | |
| D. | 小物体对半球体的压力大小为mgcosθ |
11.如图(甲)所示,直流电通过图(乙)中的电阻R,则交变电流表的示数为多少( )

| A. | 5$\sqrt{2}$A | B. | 2.5$\sqrt{2}$A | C. | 2.5A | D. | 5A |
 如图所示,质量为0.3kg的小球A放在光滑的曲面上,离地面的高度0.2m,质量为0.2kg的小球B静止在光滑水平地面上,B离竖直墙的距离d=3.5m,A静止释放,与B发生弹性碰撞,B与墙碰撞无机械能损失,不计B与墙碰撞时间,重力加速度g=10m/s2,求:
如图所示,质量为0.3kg的小球A放在光滑的曲面上,离地面的高度0.2m,质量为0.2kg的小球B静止在光滑水平地面上,B离竖直墙的距离d=3.5m,A静止释放,与B发生弹性碰撞,B与墙碰撞无机械能损失,不计B与墙碰撞时间,重力加速度g=10m/s2,求: 如图所示,有一竖直放置的U形管两臂粗细不等,左管开口向上,右管封闭着一部分气体,右管的横截面积是左管的2倍,管中装入水银,大气压为P0=76cmHg.开口管中水银面到管口距离为h1=22cm,且水银面比封闭管内高△h=4cm,封闭管内空气柱长为h2=11cm,现用小活塞把开口端封住,并缓慢推动活塞,使左侧水银面比右管内水银面高lcm,推动过程中两管的气体温度始终不变,试求:(结果保留到小数点后1位)
如图所示,有一竖直放置的U形管两臂粗细不等,左管开口向上,右管封闭着一部分气体,右管的横截面积是左管的2倍,管中装入水银,大气压为P0=76cmHg.开口管中水银面到管口距离为h1=22cm,且水银面比封闭管内高△h=4cm,封闭管内空气柱长为h2=11cm,现用小活塞把开口端封住,并缓慢推动活塞,使左侧水银面比右管内水银面高lcm,推动过程中两管的气体温度始终不变,试求:(结果保留到小数点后1位)