��Ŀ����
2��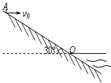 ��ͼΪ����һ���Ϊ30��Ĵ�ӵĺ����ʾ��ͼ��ˮ�����ӵĽ���ΪO��һ��վ��A�㴦���ٶ�v0��ˮƽ������Сʯ�ӣ���֪AO=40m��gȡ10m/s2������˵����ȷ���ǣ�������
��ͼΪ����һ���Ϊ30��Ĵ�ӵĺ����ʾ��ͼ��ˮ�����ӵĽ���ΪO��һ��վ��A�㴦���ٶ�v0��ˮƽ������Сʯ�ӣ���֪AO=40m��gȡ10m/s2������˵����ȷ���ǣ�������| A�� | ��ʯ�鲻������ˮ�У���v0Խ���䵽б����ʱ�ٶȷ�����б��ļн�Խ�� | |
| B�� | ��ʯ�鲻������ˮ�У���v0Խ���䵽б����ʱ�ٶȷ�����б��ļн�ԽС | |
| C�� | ��ʯ��������ˮ�У���v0Խ����ˮʱ�ٶȷ�����ˮƽ��ļн�Խ�� | |
| D�� | ��v0=18m/s����ʯ���������ˮ�� |
���� ƽ���˶���ˮƽ������������ֱ���˶�������ֱ�����������������˶������ݸ߶�����˶���ʱ�䣬���ˮƽλ�����ʯ������ˮ�е���С�ٶȣ�
ʯ��������ˮ�У�������ĸ߶�һ������ֱ���ٶ�һ�������ƽ���ı��ζ����ж��ٶȷ�����ˮƽ��н�����ٶȵĴ�С��ϵ��
ʯ�鲻������ˮ�У�ʯ����ֱλ����ˮƽλ�Ƶı�ֵ�Ƕ�ֵ�����ƽ���˶��Ĺ��ɷ�������б���ϵ��ٶȷ�����б�������ʲô�����йأ�
��� �⣺A����ʯ�鲻������ˮ�У��ٶȷ�����ˮƽ����ļнǵ�����ֵ$tan��=\frac{gt}{{v}_{0}}$��λ�Ʒ�����ˮƽ����нǵ�����ֵ$tan��=\frac{\frac{1}{2}g{t}^{2}}{{v}_{0}t}=\frac{gt}{2{v}_{0}}$����֪tan��=2tan�ȣ���Ϊ��һ�������ٶ���ˮƽ����ļн�һ������֪ʯ���䵽б��ʱ�ٶȷ�����б��ļн�һ��������ٶ��أ���A��B����
C����ʯ��������ˮ�У�������ĸ߶�һ������֪��ֱ���ٶ�һ��������$tan��=\frac{{v}_{y}}{{v}_{0}}$֪�����ٶ�Խ������ˮʱ�ٶȷ�����ˮƽ��ļн�ԽС����C����
D������h=$\frac{1}{2}g{t}^{2}$�ã�t=$\sqrt{\frac{2h}{g}}=\sqrt{\frac{2��40��\frac{1}{2}}{10}}s=2s$����ʯ������ˮ�е���С���ٶ�${v}_{0}=\frac{x}{t}=\frac{40��\frac{\sqrt{3}}{2}}{2}m/s=10\sqrt{3}m/s$��18m/s����֪v0=18m/s����ʯ���������ˮ�У���D��ȷ��
��ѡ��D��
���� �������Ĺؼ�����ƽ���˶���ˮƽ�������ֱ�����ϵ��˶����ɣ�����˶�ѧ��ʽ�����������⣮

 ������ѧ��ʱ��ҵϵ�д�
������ѧ��ʱ��ҵϵ�д� ���������ʱ��ѵϵ�д�
���������ʱ��ѵϵ�д� �㽭�¿γ���άĿ�������ʱ��ѵϵ�д�
�㽭�¿γ���άĿ�������ʱ��ѵϵ�д� ��������ϵ�д�
��������ϵ�д�| A�� | �Ʀ���=$\frac{1}{2}$�Ʀ��� | B�� | �Ʀ���=�Ʀ��� | C�� | �Ʀ���=2�Ʀ��� | D�� | �Ʀ���=4�Ʀ��� |
 ��ͼ��ʾ��С���Գ��ٶ�v0��A���ز��⻬�Ĺ���˶�����Ϊh��B����Զ����أ��䷵��;���Ծ���A�㣬ˮƽ�������б���֮����ƽ��Բ�����ӣ�ͼ��û����������A����ٶȴ�СΪ��������
��ͼ��ʾ��С���Գ��ٶ�v0��A���ز��⻬�Ĺ���˶�����Ϊh��B����Զ����أ��䷵��;���Ծ���A�㣬ˮƽ�������б���֮����ƽ��Բ�����ӣ�ͼ��û����������A����ٶȴ�СΪ��������| A�� | $\sqrt{{v}_{0}^{2}-4gh}$ | B�� | $\sqrt{4gh-{v}_{0}^{2}}$ | C�� | $\sqrt{{v}_{0}^{2}-2gh}$ | D�� | v0 |
| A�� | ���ʿ�����˹���˵ | |
| B�� | �����������ʲ�����ԶС���䱾���ߴ磬�������۲����IJ����� | |
| C�� | ������ɢ��ʵ���ǹ���ԭ�Ӻ˰뾶��ķ���֮һ | |
| D�� | �����Ƕ̵̳�ǿ����ó��� |
 ��ͼ��ʾ�����費�ơ����L=1m���㹻���Ĺ⻬��������ab��cd��ˮƽ��ɦ�=37��ǣ�����ƽ���������efhg�ڷֲ��ŴŸ�Ӧǿ�ȵĴ�СB=1T������ֱ����ƽ�����ϵ���ǿ�ų����߽�ef��gh֮��ľ���D=1.4m���ֽ�����m=0.1kg������R=$\frac{5}{3}$���ĵ����P��Q�����t=0.2s�Ⱥ�ӵ��춥���ɾ�ֹ�����ͷţ�P��Q�ڵ������˶�ʱʼ���뵼�촹ֱ�ҽӴ����ã�P����ų�ʱǡ�������˶���Q�����ų�ʱ�ٶ�Ϊ2.8m/s����֪�������ٶ�g=10m/s2��sin37��=0.6����
��ͼ��ʾ�����費�ơ����L=1m���㹻���Ĺ⻬��������ab��cd��ˮƽ��ɦ�=37��ǣ�����ƽ���������efhg�ڷֲ��ŴŸ�Ӧǿ�ȵĴ�СB=1T������ֱ����ƽ�����ϵ���ǿ�ų����߽�ef��gh֮��ľ���D=1.4m���ֽ�����m=0.1kg������R=$\frac{5}{3}$���ĵ����P��Q�����t=0.2s�Ⱥ�ӵ��춥���ɾ�ֹ�����ͷţ�P��Q�ڵ������˶�ʱʼ���뵼�촹ֱ�ҽӴ����ã�P����ų�ʱǡ�������˶���Q�����ų�ʱ�ٶ�Ϊ2.8m/s����֪�������ٶ�g=10m/s2��sin37��=0.6����
 ��ͼ��ʾ��������ͬ��ľ��A��B����ˮƽ�����ϣ�������Ϊm=1kg������B�̶�������A�����ص��滬�����������s=1.5m������Ϊ2m����С�ɺ��Ե����C����A�����ˣ�C��A֮��Ķ�Ħ������Ϊ��1=0.22��A��B��ˮƽ����֮��Ķ�Ħ������Ϊ��2=0.10�����Ħ����������Ϊ���ڻ���Ħ�������ָ�Cʩ��һ��ˮƽ���ң���СΪ0.4mg��ˮƽ����F��ʹ�俪ʼ�˶�����A��B������ײ��������ֹ���������ٶ�g=10m/s2����
��ͼ��ʾ��������ͬ��ľ��A��B����ˮƽ�����ϣ�������Ϊm=1kg������B�̶�������A�����ص��滬�����������s=1.5m������Ϊ2m����С�ɺ��Ե����C����A�����ˣ�C��A֮��Ķ�Ħ������Ϊ��1=0.22��A��B��ˮƽ����֮��Ķ�Ħ������Ϊ��2=0.10�����Ħ����������Ϊ���ڻ���Ħ�������ָ�Cʩ��һ��ˮƽ���ң���СΪ0.4mg��ˮƽ����F��ʹ�俪ʼ�˶�����A��B������ײ��������ֹ���������ٶ�g=10m/s2����  ��ͼ��ʾ������Ϊm���뾶Ϊr��С�����ڰ뾶ΪR������Ϊ3m�Ĵ�������ڣ�����ʼ��ֹ�ڹ⻬ˮƽ���ϣ���С����ͼ��λ�������ͷ����ڱڹ�����͵�ʱ��������ƶ��ľ��룮
��ͼ��ʾ������Ϊm���뾶Ϊr��С�����ڰ뾶ΪR������Ϊ3m�Ĵ�������ڣ�����ʼ��ֹ�ڹ⻬ˮƽ���ϣ���С����ͼ��λ�������ͷ����ڱڹ�����͵�ʱ��������ƶ��ľ��룮 ͬѧ�Dz���٤����ʱ����ʾƽ���˶��ķ�����������ͼ��ʾ��ʵ��װ�ã�ͼ��ˮƽ���õĵװ�����ֱ�ع̶���M���N�壮M���ϲ���һ�뾶ΪR��$\frac{1}{4}$Բ���εĴֲڹ����PΪ��ߵ㣬QΪ��͵㣬Q�㴦������ˮƽ����װ��ΪH��N���Ϲ̶�������Բ����������Ϊm��С���P����ֹ�ͷţ�С���˶���Q�ɳ������谭��ͨ����Բ�����ģ��䵽�װ��Ͼ�Qˮƽ����ΪL���������ǿ����������������ٶ�Ϊg����
ͬѧ�Dz���٤����ʱ����ʾƽ���˶��ķ�����������ͼ��ʾ��ʵ��װ�ã�ͼ��ˮƽ���õĵװ�����ֱ�ع̶���M���N�壮M���ϲ���һ�뾶ΪR��$\frac{1}{4}$Բ���εĴֲڹ����PΪ��ߵ㣬QΪ��͵㣬Q�㴦������ˮƽ����װ��ΪH��N���Ϲ̶�������Բ����������Ϊm��С���P����ֹ�ͷţ�С���˶���Q�ɳ������谭��ͨ����Բ�����ģ��䵽�װ��Ͼ�Qˮƽ����ΪL���������ǿ����������������ٶ�Ϊg����