题目内容
如图，同一竖直平面内，有两根光滑绝缘杆OA和OB，与竖直线的夹角均为45°，两杆上均套有能自由滑动的导体小球，两球的质量均为9×10-4kg，带等量同种电荷，且静止于同一竖直高度处，两球相距为L=0.2m，求：（1）两小球的电量为多少？（2）OC为AB中垂线，OC线上AB中点的电场强度是多少？（K=9×109N．m2/C2）
【答案】分析：两球均处于静止状态，合力均为零，以A球为研究对象，分析受力情况，由平衡条件求出库仑力，再由库仑定律，即可求解．
解答：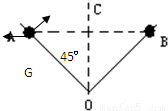
解：（1）由库仑定律得：
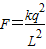①
对小球A受力分析，根据力的平行四边形定则可知，
因静止得：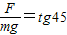
②
由①②联立解得：q=2×10-7C
（2）经分析在OC线上AB中点的场强为0
答：（1）两小球的电量为2×10-7C；
（2）OC为AB中垂线，OC线上AB中点的电场强度是零．
点评：本题是带电体平衡问题，是电场知识与力学知识的综合，库仑力是联系电场与力学两部分知识的桥梁，是要求的关键量．
解答：
解：（1）由库仑定律得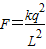：①对小球A受力分析，根据力的平行四边形定则可知，
因静止得：
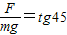②由①②联立解得：q=2×10-7C
（2）经分析在OC线上AB中点的场强为0
答：（1）两小球的电量为2×10-7C；
（2）OC为AB中垂线，OC线上AB中点的电场强度是零．
点评：本题是带电体平衡问题，是电场知识与力学知识的综合，库仑力是联系电场与力学两部分知识的桥梁，是要求的关键量．
练习册系列答案
状元坊全程突破导练测系列答案
相关题目
如图，同一竖直平面内，有两根光滑绝缘杆OA和OB，与竖直线的夹角均为45°，两杆上均套有能自由滑动的导体小球，两球的质量均为9×10-4kg，带等量同种电荷，且静止于同一竖直高度处，两球相距为L=0.2m，求：（1）两小球的电量为多少？
如图，在竖直平面内有一“v”形槽，其底部BC是一段圆弧，两侧都与光滑斜槽分别相切，相切处B、C位于同一水平面上．一小物体从右侧斜槽上距BC平面高度为2h的A处由静止开始下滑，经圆弧槽再滑上左侧斜槽，最高能到达距BC面高度为h的D点，接着小物体再向下滑回，若不考虑空气阻力，则（ ）
