题目内容
7. 某娱乐性比赛项目场地设施如图所示,水平直轨道上安装有可以载人的电动悬挂器,水面上固定一铺有海绵垫的大圆盘,半径R=1m,圆盘的圆心离平台的水平距离为L=8m,圆盘厚度不计,平台距水面高度为H=3.2m,选手在平台上双手抓住悬挂器,在电动机带动下以vo=4m/s匀速运动.在某次体验中,选手在合适的位置松手后恰能落在圆盘的圆心处(选手可看作质点,g=10m/s2).求:
某娱乐性比赛项目场地设施如图所示,水平直轨道上安装有可以载人的电动悬挂器,水面上固定一铺有海绵垫的大圆盘,半径R=1m,圆盘的圆心离平台的水平距离为L=8m,圆盘厚度不计,平台距水面高度为H=3.2m,选手在平台上双手抓住悬挂器,在电动机带动下以vo=4m/s匀速运动.在某次体验中,选手在合适的位置松手后恰能落在圆盘的圆心处(选手可看作质点,g=10m/s2).求:(1)选手刚落在圆心时的速度大小.
(2)选手若要不落在水中,松手的位置范围.
分析 (1)根据动能定理求出选手刚落在圆心时的速度大小;
(2)求出选手落在圆盘左右边界时,松手时距A的距离
解答 解:(1)根据动能定理,有:
$mgH=\frac{1}{2}m{v}_{\;}^{2}-\frac{1}{2}m{v}_{0}^{2}$
解得:$v=\sqrt{{v}_{0}^{2}+2gH}=\sqrt{{4}_{\;}^{2}+2×10×3.2}=4\sqrt{5}$m/s
(2)选手松手后做平抛运动,$H=\frac{1}{2}g{t}_{\;}^{2}$
解得:$t=\sqrt{\frac{2H}{g}}=\sqrt{\frac{2×3.2}{10}}=0.8s$
水平位移:$x={v}_{0}^{\;}t=4×0.8m=3.2m$
落在圆盘左边界时,松手位置距A距离:${x}_{1}^{\;}=L-R-x=8-1-3.2=3.8m$
落在圆盘右边界时,松手位置距A的距离:${x}_{2}^{\;}={x}_{1}^{\;}+2R=3.8+2=5,8m$
松手位置范围:3.2m≤x≤5.8m
答:(1)选手刚落在圆心时的速度大小$4\sqrt{5}m/s$.
(2)选手若要不落在水中,松手的位置范围3.2m≤x≤5.8m
点评 试题从考生感兴趣的实际情景中提炼问题,旨在考查考生对实际问题的分析、思考及物理建模的能力,倡导“让物理走进生活,让生活体现物理”的理念,养成联系实际,重视思考的好习惯.

练习册系列答案
相关题目
3. 嫦娥奔月的过程可以简化为如图所示:“嫦娥一号”升空后,绕地球沿椭圆轨道运动,远地点A距地面高为h1,然后经过变轨被月球捕获,再经多次边轨,最终在距离月球表面高为h2的轨道上绕月球做匀速圆周运动,若已知地球的半径为R1,表面重力加速度为g0,月球的质量为M,半径为R2,引力常量为G,根据以上信息,可以确定( )
嫦娥奔月的过程可以简化为如图所示:“嫦娥一号”升空后,绕地球沿椭圆轨道运动,远地点A距地面高为h1,然后经过变轨被月球捕获,再经多次边轨,最终在距离月球表面高为h2的轨道上绕月球做匀速圆周运动,若已知地球的半径为R1,表面重力加速度为g0,月球的质量为M,半径为R2,引力常量为G,根据以上信息,可以确定( )
 嫦娥奔月的过程可以简化为如图所示:“嫦娥一号”升空后,绕地球沿椭圆轨道运动,远地点A距地面高为h1,然后经过变轨被月球捕获,再经多次边轨,最终在距离月球表面高为h2的轨道上绕月球做匀速圆周运动,若已知地球的半径为R1,表面重力加速度为g0,月球的质量为M,半径为R2,引力常量为G,根据以上信息,可以确定( )
嫦娥奔月的过程可以简化为如图所示:“嫦娥一号”升空后,绕地球沿椭圆轨道运动,远地点A距地面高为h1,然后经过变轨被月球捕获,再经多次边轨,最终在距离月球表面高为h2的轨道上绕月球做匀速圆周运动,若已知地球的半径为R1,表面重力加速度为g0,月球的质量为M,半径为R2,引力常量为G,根据以上信息,可以确定( )| A. | 月球表面的重力加速度 | B. | “嫦娥一号”在远地点A时的加速度 | ||
| C. | “嫦娥一号”绕月球运动的周期 | D. | “嫦娥一号”在远地点A时的速度 |
4. 如图所示,一质点受一恒定合外力F作用从y轴上的A点平行于x轴射出,经过 一段时间到达x轴上的B点,在B点时其速度垂直于x轴指向y轴负方向,质点从A到B的过程,下列判断正确的是( )
如图所示,一质点受一恒定合外力F作用从y轴上的A点平行于x轴射出,经过 一段时间到达x轴上的B点,在B点时其速度垂直于x轴指向y轴负方向,质点从A到B的过程,下列判断正确的是( )
 如图所示,一质点受一恒定合外力F作用从y轴上的A点平行于x轴射出,经过 一段时间到达x轴上的B点,在B点时其速度垂直于x轴指向y轴负方向,质点从A到B的过程,下列判断正确的是( )
如图所示,一质点受一恒定合外力F作用从y轴上的A点平行于x轴射出,经过 一段时间到达x轴上的B点,在B点时其速度垂直于x轴指向y轴负方向,质点从A到B的过程,下列判断正确的是( )| A. | 合外力F可能向y轴负方向 | B. | 该质点的运动为匀变速运动 | ||
| C. | 该质点的速度大小可能保持不变 | D. | 该质点的速度一直在减小 |
15.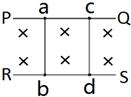 如图所示,相同的金属杆ab、cd可以在光滑金属导轨PQ和RS上滑动,空间有垂直纸面向里的匀强磁场.当ab、cd分别以速度v1和v2滑动时,发现回路感应电流为逆时针方向,则v1和v2的方向、大小可能是( )
如图所示,相同的金属杆ab、cd可以在光滑金属导轨PQ和RS上滑动,空间有垂直纸面向里的匀强磁场.当ab、cd分别以速度v1和v2滑动时,发现回路感应电流为逆时针方向,则v1和v2的方向、大小可能是( )
 如图所示,相同的金属杆ab、cd可以在光滑金属导轨PQ和RS上滑动,空间有垂直纸面向里的匀强磁场.当ab、cd分别以速度v1和v2滑动时,发现回路感应电流为逆时针方向,则v1和v2的方向、大小可能是( )
如图所示,相同的金属杆ab、cd可以在光滑金属导轨PQ和RS上滑动,空间有垂直纸面向里的匀强磁场.当ab、cd分别以速度v1和v2滑动时,发现回路感应电流为逆时针方向,则v1和v2的方向、大小可能是( )| A. | v1向右,v2向左且v1>v2 | B. | v1和v2都向左且v1>v2 | ||
| C. | v1和v2都向右且v1=v2 | D. | v1和v2都向左且v1=v2 |
2. 如图所示,清洗楼房玻璃的工人常用一根绳索将自己悬在空中,工人及其装备的总重量为G,悬绳与竖直墙壁的夹角为α,悬绳对工人的拉力大小为F1,墙壁对工人的弹力大小为F2,空中作业时工人与玻璃的水平距离为定值,则( )
如图所示,清洗楼房玻璃的工人常用一根绳索将自己悬在空中,工人及其装备的总重量为G,悬绳与竖直墙壁的夹角为α,悬绳对工人的拉力大小为F1,墙壁对工人的弹力大小为F2,空中作业时工人与玻璃的水平距离为定值,则( )
 如图所示,清洗楼房玻璃的工人常用一根绳索将自己悬在空中,工人及其装备的总重量为G,悬绳与竖直墙壁的夹角为α,悬绳对工人的拉力大小为F1,墙壁对工人的弹力大小为F2,空中作业时工人与玻璃的水平距离为定值,则( )
如图所示,清洗楼房玻璃的工人常用一根绳索将自己悬在空中,工人及其装备的总重量为G,悬绳与竖直墙壁的夹角为α,悬绳对工人的拉力大小为F1,墙壁对工人的弹力大小为F2,空中作业时工人与玻璃的水平距离为定值,则( )| A. | F1=$\frac{G}{sinα}$ | |
| B. | F2=Gcotα | |
| C. | 若缓慢增加悬绳的长度,F1减小,F2增大 | |
| D. | 在空中同一位置作业,当桶中的水不断减少,F1与F2同时减少 |
16. t=0时,甲乙两汽车从相距80km的两地开始相向行驶,它们的v一t 图象如图所示.忽略汽车掉头所需时间.下列对汽车运动状况的描述正确的是( )
t=0时,甲乙两汽车从相距80km的两地开始相向行驶,它们的v一t 图象如图所示.忽略汽车掉头所需时间.下列对汽车运动状况的描述正确的是( )
 t=0时,甲乙两汽车从相距80km的两地开始相向行驶,它们的v一t 图象如图所示.忽略汽车掉头所需时间.下列对汽车运动状况的描述正确的是( )
t=0时,甲乙两汽车从相距80km的两地开始相向行驶,它们的v一t 图象如图所示.忽略汽车掉头所需时间.下列对汽车运动状况的描述正确的是( )| A. | 在第2小时末,甲乙两车相距20 km | B. | 在第2小时末,甲乙两车相距最近 | ||
| C. | 在4小时前,两车已相遇 | D. | 在第4小时末,甲乙两车相遇 |
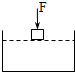 如图,用竖直向下的力将正方体木块缓慢地压入池中,木块边长为a,求从开始到木块恰好全部浸入水中浮力所做的功.已知水的密度为ρ,重力加速度为g.
如图,用竖直向下的力将正方体木块缓慢地压入池中,木块边长为a,求从开始到木块恰好全部浸入水中浮力所做的功.已知水的密度为ρ,重力加速度为g.
 在一通电直导线附近放置一个导线圆环,有三种情况:(甲)长直导线穿过导线环中心,并和导线环所在平面垂直;(乙)导线环左右对称地放在长直导线的一侧;(丙)长直导线放在导线环旁边.当长直导线中的电流减小时,导线圆环里会产生感应电流的是( )
在一通电直导线附近放置一个导线圆环,有三种情况:(甲)长直导线穿过导线环中心,并和导线环所在平面垂直;(乙)导线环左右对称地放在长直导线的一侧;(丙)长直导线放在导线环旁边.当长直导线中的电流减小时,导线圆环里会产生感应电流的是( )