题目内容
5. 如图所示,光滑水平细杆MN、CD,MN、CD在同一竖直平面内.两杆间距离为h,N、C连线左侧存在有界的电场,电场强度为E.质量为m的带正电的小球P,穿在细杆上,从M端点由静止向N端点运动,在N、C连线中点固定一个带负电的小球,电荷量为Q.在匀强电场中做匀速圆周运动恰好回到C点,且小球P与细杆之间相互绝缘.
如图所示,光滑水平细杆MN、CD,MN、CD在同一竖直平面内.两杆间距离为h,N、C连线左侧存在有界的电场,电场强度为E.质量为m的带正电的小球P,穿在细杆上,从M端点由静止向N端点运动,在N、C连线中点固定一个带负电的小球,电荷量为Q.在匀强电场中做匀速圆周运动恰好回到C点,且小球P与细杆之间相互绝缘.求:①带正电的小球P的电荷量q,
②小球P在细杆MN上滑行的末速度v0;
③光滑水平细杆M、N两点之间的电势差.
分析 由于在匀强电场中做匀速圆周运动,可以知道重力与电场力的合力为零,库仑力充当向心力,根据动能定理求电势差.
解答 解:①因带点小球做匀速圆周运动可得:
qE=mg
所以q=$\frac{mg}{E}$
②库仑力提供向心力
$\frac{KQq}{{r}^{2}}=\frac{m{V}_{0}^{2}}{r}$
h=2r
解得:V0=$\sqrt{\frac{2KQq}{hE}}$
③在细杆MN上的动能定理
$q{U}_{MN}=\frac{1}{2}m{V}_{0}^{2}$
得UMN=$\frac{4KQ}{h}$
答:①带正电的小球P的电荷量$\frac{mg}{E}$,
②小球P在细杆MN上滑行的末速度$\sqrt{\frac{2KQq}{hE}}$;
③光滑水平细杆M、N两点之间的电势差$\frac{4KQ}{h}$
点评 本题的关键是带电粒子做匀速圆周运动,分析重力与电场力的关系,结合向心力公式和动能定理求解.

练习册系列答案
相关题目
16. 如图所示,一定质量的理想气体,处在A状态时,温度为tA=27℃,则气体从状态A等容变化到状态M,再等压变化到状态B的过程中,对外所做的功W和在状态B的温度tB分别为(取1atm=1.0×105 Pa)( )
如图所示,一定质量的理想气体,处在A状态时,温度为tA=27℃,则气体从状态A等容变化到状态M,再等压变化到状态B的过程中,对外所做的功W和在状态B的温度tB分别为(取1atm=1.0×105 Pa)( )
 如图所示,一定质量的理想气体,处在A状态时,温度为tA=27℃,则气体从状态A等容变化到状态M,再等压变化到状态B的过程中,对外所做的功W和在状态B的温度tB分别为(取1atm=1.0×105 Pa)( )
如图所示,一定质量的理想气体,处在A状态时,温度为tA=27℃,则气体从状态A等容变化到状态M,再等压变化到状态B的过程中,对外所做的功W和在状态B的温度tB分别为(取1atm=1.0×105 Pa)( )| A. | W=300 J tB=27℃ | B. | W=300 J tB=-33℃ | ||
| C. | W=750 J tB=-33℃ | D. | W=750 J tB=27℃ |
13. 以不同的抛射角抛出三个小球A、B、C,三球在空中的运动轨迹如图所示,下列说法中正确的是( )
以不同的抛射角抛出三个小球A、B、C,三球在空中的运动轨迹如图所示,下列说法中正确的是( )
 以不同的抛射角抛出三个小球A、B、C,三球在空中的运动轨迹如图所示,下列说法中正确的是( )
以不同的抛射角抛出三个小球A、B、C,三球在空中的运动轨迹如图所示,下列说法中正确的是( )| A. | A、B、C三球在运动过程中,加速度都相同 | |
| B. | B球的射程最远,所以最迟落地 | |
| C. | A球的射高最大,所以最迟落地 | |
| D. | A、C两球的水平位移相等,所以两球的水平速度分量相等 |
20. 如图所示,一个质量为0.4kg的小物块从O点以v0=1m/s的初速度从水平台上的O点水平飞出,击中平台右下侧挡板上的P点.现以O为原点在竖直面内建立如图所示的平面直角坐标系,挡板的形状满足方程y=x2-6(单位:m),不计一切摩擦和空气阻力,g=10m/s2,则下列说法正确的是( )
如图所示,一个质量为0.4kg的小物块从O点以v0=1m/s的初速度从水平台上的O点水平飞出,击中平台右下侧挡板上的P点.现以O为原点在竖直面内建立如图所示的平面直角坐标系,挡板的形状满足方程y=x2-6(单位:m),不计一切摩擦和空气阻力,g=10m/s2,则下列说法正确的是( )
 如图所示,一个质量为0.4kg的小物块从O点以v0=1m/s的初速度从水平台上的O点水平飞出,击中平台右下侧挡板上的P点.现以O为原点在竖直面内建立如图所示的平面直角坐标系,挡板的形状满足方程y=x2-6(单位:m),不计一切摩擦和空气阻力,g=10m/s2,则下列说法正确的是( )
如图所示,一个质量为0.4kg的小物块从O点以v0=1m/s的初速度从水平台上的O点水平飞出,击中平台右下侧挡板上的P点.现以O为原点在竖直面内建立如图所示的平面直角坐标系,挡板的形状满足方程y=x2-6(单位:m),不计一切摩擦和空气阻力,g=10m/s2,则下列说法正确的是( )| A. | 小物块从O点运动列P点的时间为ls | |
| B. | 小物块刚到P点时速度方向与水平方向夹角的正切值等于5 | |
| C. | 小物块刚到P点时速度的大小为10m/s | |
| D. | 小物体位移大小为$\sqrt{26}$m |
17. 如图所示,圆形区域内分布着垂直纸面的匀强磁场,位于磁场边界上P点的粒子源在纸面内沿各个方向以相同的速率向磁场发射同种带电粒子,这些粒子射出边界的位置均分布在边界的某一段弧上,且这段圆弧的弧长是圆周长的$\frac{1}{3}$;若将磁感应强度的大小从B1变为B2,相应的弧长变为圆周长的$\frac{1}{6}$,则$\frac{{B}_{2}}{{B}_{1}}$等于( )
如图所示,圆形区域内分布着垂直纸面的匀强磁场,位于磁场边界上P点的粒子源在纸面内沿各个方向以相同的速率向磁场发射同种带电粒子,这些粒子射出边界的位置均分布在边界的某一段弧上,且这段圆弧的弧长是圆周长的$\frac{1}{3}$;若将磁感应强度的大小从B1变为B2,相应的弧长变为圆周长的$\frac{1}{6}$,则$\frac{{B}_{2}}{{B}_{1}}$等于( )
 如图所示,圆形区域内分布着垂直纸面的匀强磁场,位于磁场边界上P点的粒子源在纸面内沿各个方向以相同的速率向磁场发射同种带电粒子,这些粒子射出边界的位置均分布在边界的某一段弧上,且这段圆弧的弧长是圆周长的$\frac{1}{3}$;若将磁感应强度的大小从B1变为B2,相应的弧长变为圆周长的$\frac{1}{6}$,则$\frac{{B}_{2}}{{B}_{1}}$等于( )
如图所示,圆形区域内分布着垂直纸面的匀强磁场,位于磁场边界上P点的粒子源在纸面内沿各个方向以相同的速率向磁场发射同种带电粒子,这些粒子射出边界的位置均分布在边界的某一段弧上,且这段圆弧的弧长是圆周长的$\frac{1}{3}$;若将磁感应强度的大小从B1变为B2,相应的弧长变为圆周长的$\frac{1}{6}$,则$\frac{{B}_{2}}{{B}_{1}}$等于( )| A. | 2 | B. | $\sqrt{2}$ | C. | 3 | D. | $\sqrt{3}$ |
15.下列说法正确的是 ( )
| A. | 分子间的距离增大时,分子势能一定增大 | |
| B. | 晶体有确定的熔点,非晶体没有确定的熔点 | |
| C. | 热量总是白发地从分子平均动能大的物体传递到分子平均动能小的物体 | |
| D. | 物体吸热时,它的内能一定增加 | |
| E. | 一定质量的理想气体,如果压强不变,体积增大,那么它一定从外界吸热 |
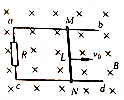 如图所示,两条平行金属导轨ab、cd置于匀强磁场中,磁场方向垂直金属导轨平面,两导轨间的距离L=0.6m,金属杆MN沿两条导轨向右匀速滑动,速度v0=10m/s,产生的感应电动势为3V,已知金属到杆MN的电阻r=1Ω,外接电阻R=8Ω.求:
如图所示,两条平行金属导轨ab、cd置于匀强磁场中,磁场方向垂直金属导轨平面,两导轨间的距离L=0.6m,金属杆MN沿两条导轨向右匀速滑动,速度v0=10m/s,产生的感应电动势为3V,已知金属到杆MN的电阻r=1Ω,外接电阻R=8Ω.求:
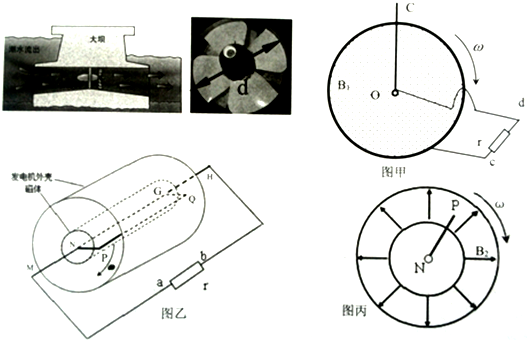
 ”形状金属杆MNPQGH在辐向磁场中也以角速度ω匀速转动,如图乙所示,图丙为发电机的截面图,已知NP=GQ=R,PQ=L,MH两端接入电阻r,其余电阻不计.
”形状金属杆MNPQGH在辐向磁场中也以角速度ω匀速转动,如图乙所示,图丙为发电机的截面图,已知NP=GQ=R,PQ=L,MH两端接入电阻r,其余电阻不计.