题目内容
11. 如图所示,MN、PQ为平行光滑导轨,其电阻忽略不计,与地面成30°角固定.N、Q间接一电阻R′=1.0Ω,M、P端与电池组和开关组成回路,电动势E=6V,内阻r=1.0Ω,导轨区域加有与两导轨所在平面垂直的匀强磁场.现将一条质量m=0.04kg,电阻R=1.0Ω的金属导线置于导轨上,并保持导线ab水平.已知导轨间距L=0.1m,当开关S接通后导线ab恰静止不动.试计算磁感应强度大小.
如图所示,MN、PQ为平行光滑导轨,其电阻忽略不计,与地面成30°角固定.N、Q间接一电阻R′=1.0Ω,M、P端与电池组和开关组成回路,电动势E=6V,内阻r=1.0Ω,导轨区域加有与两导轨所在平面垂直的匀强磁场.现将一条质量m=0.04kg,电阻R=1.0Ω的金属导线置于导轨上,并保持导线ab水平.已知导轨间距L=0.1m,当开关S接通后导线ab恰静止不动.试计算磁感应强度大小.
分析 导体杆静止在导轨上,受到重力、支持力和安培力三个力作用,根据平衡条件和闭合电路欧姆定律结合安培力大小为F=BIL,即可求得磁感应强度.
解答 解:开关S接通后电路的总电阻为 R总=$\frac{RR′}{R+R′}$+r=$\frac{1×1}{1+1}$+1=1.5Ω
根据闭合电路欧姆定律和并联电路的特点,有:
通过ab中的电流 I=$\frac{1}{2}•\frac{E}{{R}_{总}}$=$\frac{1}{2}×\frac{6}{1.5}$A=2A
由于导线ab静止不动,受力平衡,由受力分析,有:
BIL=mgsinθ
可得 B=$\frac{mgsin30°}{IL}$=$\frac{0.04×10×0.5}{2×0.1}$T=1T
答:磁感应强度大小为1T.
点评 本题是力电综合问题,关键是分析清楚电路结构、受力情况、能量转化情况,然后根据平衡条件、闭合电路欧姆定律和法拉第电磁感应定律列式求解.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
1. 如图所示,竖直绝缘墙壁上有一固定的质点A,在A的正上方的P点用丝线悬挂另一质点B,A、B两质点因为带电而相互排斥,致使悬线与竖直方向成θ角,由于漏电使A、B两质点的电荷量逐渐减少,在电荷漏电完毕之前悬线对悬点P的拉力大小( )
如图所示,竖直绝缘墙壁上有一固定的质点A,在A的正上方的P点用丝线悬挂另一质点B,A、B两质点因为带电而相互排斥,致使悬线与竖直方向成θ角,由于漏电使A、B两质点的电荷量逐渐减少,在电荷漏电完毕之前悬线对悬点P的拉力大小( )
 如图所示,竖直绝缘墙壁上有一固定的质点A,在A的正上方的P点用丝线悬挂另一质点B,A、B两质点因为带电而相互排斥,致使悬线与竖直方向成θ角,由于漏电使A、B两质点的电荷量逐渐减少,在电荷漏电完毕之前悬线对悬点P的拉力大小( )
如图所示,竖直绝缘墙壁上有一固定的质点A,在A的正上方的P点用丝线悬挂另一质点B,A、B两质点因为带电而相互排斥,致使悬线与竖直方向成θ角,由于漏电使A、B两质点的电荷量逐渐减少,在电荷漏电完毕之前悬线对悬点P的拉力大小( )| A. | 变小 | B. | 变大 | C. | 不变 | D. | 无法确定 |
2. 如图所示,带电金属小球用绝缘丝线系住,丝线上端固定,形成一个摆,如果在摆球经过的区域加上如图所示的磁场,不计摩擦及空气阻力,下列说法中不正确的是( )
如图所示,带电金属小球用绝缘丝线系住,丝线上端固定,形成一个摆,如果在摆球经过的区域加上如图所示的磁场,不计摩擦及空气阻力,下列说法中不正确的是( )
 如图所示,带电金属小球用绝缘丝线系住,丝线上端固定,形成一个摆,如果在摆球经过的区域加上如图所示的磁场,不计摩擦及空气阻力,下列说法中不正确的是( )
如图所示,带电金属小球用绝缘丝线系住,丝线上端固定,形成一个摆,如果在摆球经过的区域加上如图所示的磁场,不计摩擦及空气阻力,下列说法中不正确的是( )| A. | 摆球每次通过最低点时丝线拉力大小不相等 | |
| B. | 摆球每次通过最低点时动能相等 | |
| C. | 摆球每次离开最低点时的最大距离逐渐减少 | |
| D. | 摆球每次在上丝线最大偏角处丝线的拉力大小不变 |
19. 用两辆拖拉机拉一辆陷入泥坑的卡车,如图所示,一辆拖拉机沿与卡车前进方向成45°角、用大小为1000$\sqrt{2}$N的力F1拉卡车,另一辆拖拉机沿与卡车前进方向成30°、用大小为2×103N的力F2拉卡车,卡车开动后自身向前提供的动力为4×103N,三车同时作用,刚好使卡车脱离泥坑,则卡车受到的阻力约为( )
用两辆拖拉机拉一辆陷入泥坑的卡车,如图所示,一辆拖拉机沿与卡车前进方向成45°角、用大小为1000$\sqrt{2}$N的力F1拉卡车,另一辆拖拉机沿与卡车前进方向成30°、用大小为2×103N的力F2拉卡车,卡车开动后自身向前提供的动力为4×103N,三车同时作用,刚好使卡车脱离泥坑,则卡车受到的阻力约为( )
 用两辆拖拉机拉一辆陷入泥坑的卡车,如图所示,一辆拖拉机沿与卡车前进方向成45°角、用大小为1000$\sqrt{2}$N的力F1拉卡车,另一辆拖拉机沿与卡车前进方向成30°、用大小为2×103N的力F2拉卡车,卡车开动后自身向前提供的动力为4×103N,三车同时作用,刚好使卡车脱离泥坑,则卡车受到的阻力约为( )
用两辆拖拉机拉一辆陷入泥坑的卡车,如图所示,一辆拖拉机沿与卡车前进方向成45°角、用大小为1000$\sqrt{2}$N的力F1拉卡车,另一辆拖拉机沿与卡车前进方向成30°、用大小为2×103N的力F2拉卡车,卡车开动后自身向前提供的动力为4×103N,三车同时作用,刚好使卡车脱离泥坑,则卡车受到的阻力约为( )| A. | 8.2×103 N | B. | 6.0×103 N | C. | 5.6×103 N | D. | 6.7×103 N |
6. 电源、开关S、定值电阻R1、光敏电阻R2和电容器连接成如图所示电路,电容器的两平行板水平放置.当开关S闭合,并且无光照射光敏电阻R2时,一带电液滴恰好静止在电容器两板间的M点.当用强光照射光敏电阻R2时,则( )
电源、开关S、定值电阻R1、光敏电阻R2和电容器连接成如图所示电路,电容器的两平行板水平放置.当开关S闭合,并且无光照射光敏电阻R2时,一带电液滴恰好静止在电容器两板间的M点.当用强光照射光敏电阻R2时,则( )
 电源、开关S、定值电阻R1、光敏电阻R2和电容器连接成如图所示电路,电容器的两平行板水平放置.当开关S闭合,并且无光照射光敏电阻R2时,一带电液滴恰好静止在电容器两板间的M点.当用强光照射光敏电阻R2时,则( )
电源、开关S、定值电阻R1、光敏电阻R2和电容器连接成如图所示电路,电容器的两平行板水平放置.当开关S闭合,并且无光照射光敏电阻R2时,一带电液滴恰好静止在电容器两板间的M点.当用强光照射光敏电阻R2时,则( )| A. | 液滴向下运动 | B. | 液滴向上运动 | ||
| C. | 电容器所带电荷量减少 | D. | 电容器两极板间电压变大 |
16.关于路程和位移,下列说法正确的是( )
| A. | 物体通过的路程不同,但位移可能相同 | |
| B. | 物体沿某一直线运动,所通过的路程就是位移 | |
| C. | 物体的位移为零,则物体一定没运动 | |
| D. | 物体通过一段路程以后,位移必定发生变化 |
20.关于多普勒效应,下列说法正确的是( )
| A. | 多普勒效应是由波的干涉引起的 | |
| B. | 多普勒效应是由于波源和观察者之间有相对运动而产生的 | |
| C. | 多普勒效应不能说明波源的频率发生了变化 | |
| D. | 声波可以产生多普勒效应 |
 长度为L=0.4m,一端固定一小球,另一端固定在转动轴O上,小球绕轴在竖直平面内转动.杆的质量忽略不计,小球的质量为0.5kg.(g=10m/s2)求
长度为L=0.4m,一端固定一小球,另一端固定在转动轴O上,小球绕轴在竖直平面内转动.杆的质量忽略不计,小球的质量为0.5kg.(g=10m/s2)求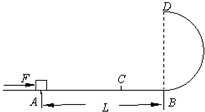 如图所示,固定在竖直面内的光滑半圆形轨道与粗糙水平轨道在B点平滑连接.轨道半径R=0.5m,一质量m=0.2kg的小物块(可视为质点)放在水平轨道上的A点,A与B相距L=10m,物块与水平轨道间的动摩擦因数μ=0.1.现用一水平恒力F向右推物块.已知F=3N,当物块运动到C点时撤去该力,设C点到A点的距离为x.在圆轨道的最高点D处安装一压力传感器,当物块运动到D点时传感器就会显示相应的读数FN,压力传感器所能承受的最大压力为90N,g取10m/s2.求:要使物块能够通过圆轨道的最高点D,求x的范围.
如图所示,固定在竖直面内的光滑半圆形轨道与粗糙水平轨道在B点平滑连接.轨道半径R=0.5m,一质量m=0.2kg的小物块(可视为质点)放在水平轨道上的A点,A与B相距L=10m,物块与水平轨道间的动摩擦因数μ=0.1.现用一水平恒力F向右推物块.已知F=3N,当物块运动到C点时撤去该力,设C点到A点的距离为x.在圆轨道的最高点D处安装一压力传感器,当物块运动到D点时传感器就会显示相应的读数FN,压力传感器所能承受的最大压力为90N,g取10m/s2.求:要使物块能够通过圆轨道的最高点D,求x的范围.