题目内容
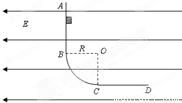
如图为一固定在竖直平面内的绝缘轨道,AB部分为竖直,CD部分为水平,BC为与它们相切的四分之一圆弧,半径为R.空间存在水平方向匀强电场,场强方向与ABCD所在平面平行.有一小物块,质量为m、电量为q,自AB上离B点距离R处自由释放后沿轨道运动到CD上离C点距离R处并返回…已知物块与轨道的竖直、水平部分的摩擦因数均为μ=0.5,轨道的圆弧部分为光滑.(1)求匀强电场的场强E多大?
(2)求上述过程中物块第一次向左经过圆弧上C点时,对于轨道的压力;
(3)计算物块第一、二两次经过C点所间隔的时间;
(4)物块最终将在哪个范围内运动(要求写出边界位置与O点的连线跟OC所成夹角θ的余弦).
【答案】分析:(1)A-B-C-D的过程中,重力、电场力和摩擦力做功,初、末速度均为0,可以使用动能定律;(2)D-C先使用动能定律求出速度,再代入向心力的公式,可以求出对轨道的压力;(3)C-D-C的过程,物体在电场力和摩擦力的作用下,先减速后加速,两段的合力不同,应分别求出加速度,计算出两次的时间,加在一起;
(4)范围可以根据受力的关系和能量的转化与守恒来确定.
解答:解:(1)A-D的过程中,重力、电场力和摩擦力做功,由动能定律得:
2mgR-2qER-μmgR-μqER=0
所以: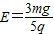
(2)设再次到达C时,物体的速度是v,D-C电场力和摩擦力做功,由动能定律:
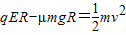
在C点支持力与重力的合力提供向心力:

代入数据,解得:FN=1.2mg
因此,所求压力的大小为1.2mg
(3)分别用a1和t1表示所求过程中物块向右运动加速度大小和时间,则:
 ,
,
分别用a2和t2表示所求过程中物块向左运动加速度大小和时间,则:
 ,
,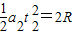
又:t=t1+t2
代入数据,解得:
(4)由(1)可知,重力大于电场力,故物体运动的右边界为C点,从点到最左端,由动能定律:
qERsinθ-mgR(1-cosθ)=0
可得: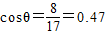
答:(1)电场强度 ;
;
(2)压力为1.2mg;
(3)再次到达C点的时间: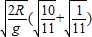 ;
;
(4)物体运动的范围在c点到cosθ=0.47的点之间.
点评:该题带电物体在重力与电场的复合场中的运动,涉及到动能定律、圆周运动等知识点,属于较难的题目.
(4)范围可以根据受力的关系和能量的转化与守恒来确定.
解答:解:(1)A-D的过程中,重力、电场力和摩擦力做功,由动能定律得:
2mgR-2qER-μmgR-μqER=0
所以:
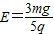
(2)设再次到达C时,物体的速度是v,D-C电场力和摩擦力做功,由动能定律:
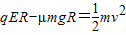
在C点支持力与重力的合力提供向心力:

代入数据,解得:FN=1.2mg
因此,所求压力的大小为1.2mg
(3)分别用a1和t1表示所求过程中物块向右运动加速度大小和时间,则:
 ,
,
分别用a2和t2表示所求过程中物块向左运动加速度大小和时间,则:
 ,
,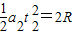
又:t=t1+t2
代入数据,解得:

(4)由(1)可知,重力大于电场力,故物体运动的右边界为C点,从点到最左端,由动能定律:
qERsinθ-mgR(1-cosθ)=0
可得:
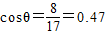
答:(1)电场强度
 ;
;(2)压力为1.2mg;
(3)再次到达C点的时间:
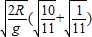 ;
;(4)物体运动的范围在c点到cosθ=0.47的点之间.
点评:该题带电物体在重力与电场的复合场中的运动,涉及到动能定律、圆周运动等知识点,属于较难的题目.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 (2011?绍兴二模)一端弯曲的光滑绝缘杆ABD固定在竖直平面上,如图所示,AB段水平,BD段是半径为R的半圆弧,有电荷量为Q(Q>0)的点电荷固定在圆心O点.一质量为m、电荷量为q(q>0)的带电小环套在光滑绝缘杆上,在水平外力作用下从C点由静此开始运动,到B点时撤去外力,小环继续运动,发现刚好能到绝缘杆的最高点D.已知CB间距为4R/3.(提示:根据电磁学有关知识,在某一空间放一电荷量为Q的点电荷,则距离点电荷为r的某点的电势为
(2011?绍兴二模)一端弯曲的光滑绝缘杆ABD固定在竖直平面上,如图所示,AB段水平,BD段是半径为R的半圆弧,有电荷量为Q(Q>0)的点电荷固定在圆心O点.一质量为m、电荷量为q(q>0)的带电小环套在光滑绝缘杆上,在水平外力作用下从C点由静此开始运动,到B点时撤去外力,小环继续运动,发现刚好能到绝缘杆的最高点D.已知CB间距为4R/3.(提示:根据电磁学有关知识,在某一空间放一电荷量为Q的点电荷,则距离点电荷为r的某点的电势为 一端弯曲的光滑绝缘轨道ABD固定在竖直平面上,如图所示,AB段水平、BD段是半径为R的半圆弧,有电荷量为Q的正点电荷固定在圆心O处.一质量为m、电荷量为q的带正电小环,在水平恒力F0作用下从C点由静止开始运动,到B点时撤去外力,小环继续运动,发现刚好能到达绝缘轨道上与圆心等高的M点,已知CB间距为
一端弯曲的光滑绝缘轨道ABD固定在竖直平面上,如图所示,AB段水平、BD段是半径为R的半圆弧,有电荷量为Q的正点电荷固定在圆心O处.一质量为m、电荷量为q的带正电小环,在水平恒力F0作用下从C点由静止开始运动,到B点时撤去外力,小环继续运动,发现刚好能到达绝缘轨道上与圆心等高的M点,已知CB间距为 (2008?如皋市模拟)如图所示,一绝缘细圆环半径为 r,其环面固定在竖直平面上,方向水平向右、场强大小为E的匀强电场与圆环平面平行,环上穿有一电荷量为+q 的小球,可沿圆环做无摩擦的圆周运动,若小球经A点时速度方向恰与电场方向垂直,且圆环与小球间沿水平方向无力的作用.小球沿顺时针方向运动,且qE=mg,求小球运动到何处时,对环的作用力最大?最大作用力为多大?
(2008?如皋市模拟)如图所示,一绝缘细圆环半径为 r,其环面固定在竖直平面上,方向水平向右、场强大小为E的匀强电场与圆环平面平行,环上穿有一电荷量为+q 的小球,可沿圆环做无摩擦的圆周运动,若小球经A点时速度方向恰与电场方向垂直,且圆环与小球间沿水平方向无力的作用.小球沿顺时针方向运动,且qE=mg,求小球运动到何处时,对环的作用力最大?最大作用力为多大?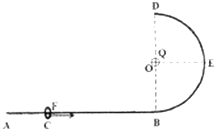 一端弯曲的光滑绝缘杆ABD固定在竖直平面上,如图所示,AB段水平,BD段是半径为R的半圆弧,有一电荷量为Q的正点电荷固定在圆心O点.一质量为m、电荷量为q的带正电小环套在光滑绝缘杆上,在大小为F的水平恒力作用下从C点由静止开始运动,到B点时撤去恒力,小环继续运动到达D点,已知CB间距为
一端弯曲的光滑绝缘杆ABD固定在竖直平面上,如图所示,AB段水平,BD段是半径为R的半圆弧,有一电荷量为Q的正点电荷固定在圆心O点.一质量为m、电荷量为q的带正电小环套在光滑绝缘杆上,在大小为F的水平恒力作用下从C点由静止开始运动,到B点时撤去恒力,小环继续运动到达D点,已知CB间距为