题目内容
7. 如图所示,极板间距为d、长为L的平行板电容器水平固定放置,与电动势为E的电源相连,一质量为m的带电小球P在a、b间的电场内的正中心保持静止,现设法使P固定,再使两平行金属板a、b分别以中心点0、O′为轴转一个相同的小角度θ(转动后两极板依然可认为是正对的),保持电源与电容器的连接状态不变,然后释放小球P,已知小球可视为点电荷,其带电荷量不会影响平行板电容器的电荷分布.
如图所示,极板间距为d、长为L的平行板电容器水平固定放置,与电动势为E的电源相连,一质量为m的带电小球P在a、b间的电场内的正中心保持静止,现设法使P固定,再使两平行金属板a、b分别以中心点0、O′为轴转一个相同的小角度θ(转动后两极板依然可认为是正对的),保持电源与电容器的连接状态不变,然后释放小球P,已知小球可视为点电荷,其带电荷量不会影响平行板电容器的电荷分布.(1)试求带电小球P的电性及电荷量;
(2)释放后的小球P在电场中做什么性质的运动?请确定相关的物理量.
分析 (1)带电小球P在a、b间静止时,重力与电场力平衡,由平衡条件分析P球的电性,并求得其电荷量.
(2)释放后的小球P在电场中,由于电场改变了方向,电场力随之改变,小球P将开始运动,由牛顿第二定律求出加速度.
解答  解:(1)带电小球P在a、b间静止时,重力与电场力平衡,则电场力方向竖直向上,而电场方向竖直向下,所以小球P带负电.
解:(1)带电小球P在a、b间静止时,重力与电场力平衡,则电场力方向竖直向上,而电场方向竖直向下,所以小球P带负电.
由平衡条件得:
q$\frac{E}{d}$=mg
则得:q=$\frac{mgd}{E}$
(2)使两平行金属板a、b分别以中心点0、O′为轴转一个相同的小角度θ,然后释放P,此时P受到竖直向下的重力、垂直金属板的电场力,电场力方向与竖直方向的夹角为θ,如图.
板间距离原来为d,由几何知识得知:转过θ角时,板间距离为dcosθ,板间场强为:E电=$\frac{E}{dcosθ}$
P受到的电场力为:F=qE电=$\frac{qE}{dcosθ}$
电场力方向与竖直方向的夹角为θ,竖直方向的分力为:Fcosθ=$\frac{qE}{d}$.
可得:Fcosθ=mg
所以小球的合力水平向右,大小为:Fsinθ=$\frac{qEtanθ}{d}$
则其加速度为:a=$\frac{Fsinθ}{m}$=$\frac{qEtanθ}{md}$
故P将水平向右作加速度为$\frac{qEtanθ}{md}$的匀加速直线运动.
答:(1)小球P带负电,电荷量为$\frac{mgd}{E}$.
(2)P将水平向右作加速度为$\frac{qEtanθ}{md}$的匀加速直线运动.
点评 此题考查了已知受力求运动,正确受力分析,根据牛顿第二定律判断运动情况.要注意板间的电压不变,而板间距离是变化的,场强随之变化.

练习册系列答案
 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
15.如图所示为甲、乙两物体做直线运动的v-t图线,由图知( )
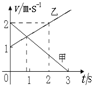

| A. | 甲、乙两物体都做匀变速直线运动 | B. | 0~1s内甲和乙的位移相同 | ||
| C. | 甲和乙的加速度方向相同 | D. | 甲和乙的运动方向相反 |
2.平台高h=5m,小球以v0=10m/s的速度水平抛出,(g=10m/s2)忽略空气阻力,则( )


| A. | 小球落地时间为2s | |
| B. | 小球落地时水平位移10m | |
| C. | 小球落地时速度大小 20m/s | |
| D. | 小球落地时速度方向与水平方向成60° |
12.一个单匝矩形线框的面积为S,在磁感应强度为B的匀强磁场中,从线圈平面与磁场垂直的位置开始计时,转速为n转/秒,则( )
| A. | 线框交变电动势的最大值为nπBS | |
| B. | 每秒内感应电流方向就改变2n次 | |
| C. | 线框在中性面感应电流最大 | |
| D. | 感应电动势瞬时值为e=2πBSsin2nπt |
6. 如图所示,物体以100J的初动能从斜面的底端向上运动,斜面足够长.当它向上通过斜面上的M点时,其动能减少了75J,机械能减少了30J.如果以地面为零势能参考面,物体能从斜面上返回底端,则( )
如图所示,物体以100J的初动能从斜面的底端向上运动,斜面足够长.当它向上通过斜面上的M点时,其动能减少了75J,机械能减少了30J.如果以地面为零势能参考面,物体能从斜面上返回底端,则( )
 如图所示,物体以100J的初动能从斜面的底端向上运动,斜面足够长.当它向上通过斜面上的M点时,其动能减少了75J,机械能减少了30J.如果以地面为零势能参考面,物体能从斜面上返回底端,则( )
如图所示,物体以100J的初动能从斜面的底端向上运动,斜面足够长.当它向上通过斜面上的M点时,其动能减少了75J,机械能减少了30J.如果以地面为零势能参考面,物体能从斜面上返回底端,则( )| A. | 物体在向上运动过程中,机械能减少100J | |
| B. | 物体到达斜面上最高点时时,重力势能增加了60J | |
| C. | 物体返回斜面底端时动能为40J | |
| D. | 物体返回M点时机械能为50J |
4.一重为10N的物体置于水平地面上.现用测力计拉住物体使其匀速拉出,测力计的读数为1N,则物体与纸带间的动摩擦因数是( )
| A. | 1 | B. | 0.1 | C. | 10 | D. | 0.01 |
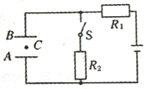 如图所示电路,电源内阻r=1Ω,电阻R1=4Ω,A、B是水平放置的平行板电容器,当开关S断开时,一电子从A板由静止飞到B板时的速度为v0,当开关S闭合时,电子从A由静止飞到B板的过程中,通过两板的中点C的速度为$\frac{\sqrt{3}}{3}$v0,求R2的阻值.
如图所示电路,电源内阻r=1Ω,电阻R1=4Ω,A、B是水平放置的平行板电容器,当开关S断开时,一电子从A板由静止飞到B板时的速度为v0,当开关S闭合时,电子从A由静止飞到B板的过程中,通过两板的中点C的速度为$\frac{\sqrt{3}}{3}$v0,求R2的阻值.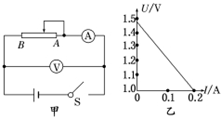 为了测量一节干电池的电动势和内阻,某实验小组按图甲所示的电路图连好实验电路,合上开关,电流表和电压表的均有读数.当将滑动变阻器的滑片由A端向B端逐渐滑动时,开始一段时间内,发现电流表的示数一直都很小,而电压表的示数接近1.5V且几乎不变,直到当滑片滑至临近B端时,电压表和电流表的示数才急剧变化,出现上述情况的原因是滑动变阻器的全阻值太大;有效使用的部分短.改进方法是换用全阻值小的滑动变阻器.改进后,测出几组电流、电压的数值,并画出如图乙所示的图象,由图象可知,这个电池的电动势为E=1.46V,内阻r=2.3Ω.
为了测量一节干电池的电动势和内阻,某实验小组按图甲所示的电路图连好实验电路,合上开关,电流表和电压表的均有读数.当将滑动变阻器的滑片由A端向B端逐渐滑动时,开始一段时间内,发现电流表的示数一直都很小,而电压表的示数接近1.5V且几乎不变,直到当滑片滑至临近B端时,电压表和电流表的示数才急剧变化,出现上述情况的原因是滑动变阻器的全阻值太大;有效使用的部分短.改进方法是换用全阻值小的滑动变阻器.改进后,测出几组电流、电压的数值,并画出如图乙所示的图象,由图象可知,这个电池的电动势为E=1.46V,内阻r=2.3Ω.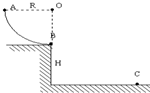 如图所示,质量为10kg的小球,从竖直圆弧轨道的A点由静止释放,沿$\frac{1}{4}$圆弧轨道运动至最低点B后飞出,落在水平面上的C点,已知圆弧半径为R=12m,小球落到C点时速度的大小为 vC=25m/s,B点离水平面高度为H=20m,不计空气阻力,g取10m/s2,求:
如图所示,质量为10kg的小球,从竖直圆弧轨道的A点由静止释放,沿$\frac{1}{4}$圆弧轨道运动至最低点B后飞出,落在水平面上的C点,已知圆弧半径为R=12m,小球落到C点时速度的大小为 vC=25m/s,B点离水平面高度为H=20m,不计空气阻力,g取10m/s2,求: