题目内容
5.如图所示,质量M=2m的平板车B上放有一个质量为m的小滑块A.平板车静止于光滑的水平面上,小滑块与车面间的动摩擦因数为μ,现给车施加一个水平向右的瞬间冲量,使车向右运动,同时小滑块相对于小车滑动,当二者达到共同速度v之后一起向前运动,设平板车足够长,重力加速度为g.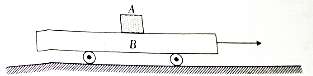
求:(1)给车施加的水平向右的瞬间冲量的大小;
(2)小滑块A在平板车B上滑过的距离.
分析 (1)对AB整体,由动量定理列方程求解;
(2)再由能量守恒列方程求整个过程中滑块A相对平板车B滑动的总路程;
解答 解:(1)设瞬间冲量为I,对AB整体由动量定理得:
I=(M+m)v
解得:I=3mv
(2)设水平向右的方向为正方向,根据动量守恒,则B的初速度为
Mv0=(M+m)v
v0=1.5v
设整个过程中滑块A相对平板车B滑动的总路程为s,对AB整体由能量守恒定律得:
-μmgs=$\frac{1}{2}$(M+m)v2-$\frac{1}{2}$Mv${\;}_{0}^{2}$
联立解得:s=$\frac{3{v}^{2}}{4μg}$
答:(1)给车施加的水平向右的瞬间冲量的大小为3mv;
(2)小滑块A在平板车B上滑过的距离 $\frac{3{v}^{2}}{4μg}$
点评 解决本题的关键理清A、B的运动过程,抓住AB系统动量守恒,结合动量守恒定律和能量守恒定律进行求解.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
16.一条小船在静水中的速度为10m/s,要渡过宽度为60m、水流速度为6m/s的河流,下列说法正确的是( )
| A. | 小船渡河的最短时间为6 s | |
| B. | 小船渡河的最短时间为10 s | |
| C. | 小船渡河的路程最短时,渡河时间为7.5 s | |
| D. | 若小船在静水中的速度增加,则小船渡河的最短路程减小 |
20.下列说法中正确的是( )
| A. | 做曲线运动的物体受到的合外力可以为零 | |
| B. | 在恒力作用下,物体不可能做曲线运动 | |
| C. | 在变力作用下,物体一定做曲线运动 | |
| D. | 曲线运动一定是变速运动 |
20.已知下面的哪组数据,可以算出地球的质量M(引力常量G为已知)( )
| A. | 地球绕太阳运行的周期T2及地球到太阳中心的距离r2 | |
| B. | 月球绕地球运行的周期T1及月球到地球中心的距离r1 | |
| C. | 人造卫星在地面附近的运行速度v3和运行周期T3 | |
| D. | 地球绕太阳运行的速度v4及地球到太阳中心的距离r4 |
1.互联网正在极大地促进商业的发展和消费的升级,“020”模式是指将线下的商务机会与互联网结合,让互联网成为线下交易的前台的一种商业新模式.具体到一家外卖公与消费者之间,就是消费者在网络平合上下单订购,而公司进行线下的配送服务.某外卖公司为了更好地为消费者服务,配送员工使用的是“XR-2016”型电动自行车工作,以下是该车的相关参数:
该电动自行车采用后轮驱动直流电动机,其中额定转速是电动自行车在满载情况下在平直公路上以额定功率匀速行进时的巿轮转速,求:
(1)电动自行车以额定转速行进时的速度v0;在额定工作状态时,损失的功率有80%是由于电动机绕线电阻生热而产生的,则电动机的绕线电阻为多大;
(2)满载情况下,该车以速度v=5m/s沿着坡度为θ=4.59°的长直坡道向上匀速行驶时,受到的摩擦阻力为车重(含载重)重量的0.02倍,求此状态下电动自行车实际运行机械功率(sin 4.59°=0.08;重力加速度g=10 m/s2).
| 名称 | 车身 质量 | 满载 载重 | 前后车轮直径 | 额定 转速 | 电动机额定电压 | 电动机额定电流 | 额定机械输出功率 |
| 参数 | 40kg | 80kg | 40cm | $\frac{4500}{2π}$r/min | 48V | 20A | 835W |
(1)电动自行车以额定转速行进时的速度v0;在额定工作状态时,损失的功率有80%是由于电动机绕线电阻生热而产生的,则电动机的绕线电阻为多大;
(2)满载情况下,该车以速度v=5m/s沿着坡度为θ=4.59°的长直坡道向上匀速行驶时,受到的摩擦阻力为车重(含载重)重量的0.02倍,求此状态下电动自行车实际运行机械功率(sin 4.59°=0.08;重力加速度g=10 m/s2).


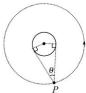 如图所示,飞行器P绕某星球做匀速圆周运动周期为T,已知星球相对飞行器的张角为θ,引力常量为G.求该星球的密度?
如图所示,飞行器P绕某星球做匀速圆周运动周期为T,已知星球相对飞行器的张角为θ,引力常量为G.求该星球的密度?