题目内容
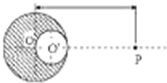
质量为M的均匀实心球的半径为R,中心为O点.现在设想在里面造成一个球形空腔,其半径为,中心为O1,球形空腔与均匀实心球相切,在OO1的连线上与O点相距为L>R的P点,放一个质量为m的质点,则球的剩余部分对此质点的引力F=______.

其内部挖去一个半径为0.5R的球形空穴,挖去小球的质量为:m′=(
)3M=0.125M,
故挖去前的引力为:F=G
被挖部分对质点的引力为:F′=G
,
剩余部分的引力为:F-F′=GMm(
-
)
答:剩余部分对m2的万有引力为GMm(
-
)
| 0.5R |
| R |
故挖去前的引力为:F=G
| Mm |
| L2 |
被挖部分对质点的引力为:F′=G
| 0.125Mm |
| (L-0.5R)2 |
剩余部分的引力为:F-F′=GMm(
| 1 |
| L2 |
| 1 |
| 8(L-0.5R)2 |
答:剩余部分对m2的万有引力为GMm(
| 1 |
| L2 |
| 1 |
| 8(L-0.5R)2 |

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目

