题目内容
20.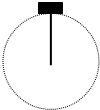 长为0.4m、质量可忽略的杆,其下端固定于O点,上端连接着一个零件A,A的质量为m=2kg,它绕O点在竖直平面内做圆周运动,如图所示,求在下列两种情况下杆在最高点受的力:
长为0.4m、质量可忽略的杆,其下端固定于O点,上端连接着一个零件A,A的质量为m=2kg,它绕O点在竖直平面内做圆周运动,如图所示,求在下列两种情况下杆在最高点受的力:(1)A最高点的速率为1m/s;
(2)A最高点的速率为4m/s.(g取10m/s2)
分析 小球在最高点,靠杆子的作用力和重力的合力提供向心力,根据牛顿第二定律求出作用力的大小和方向.
解答 解:设杆长为L,在最高点速度为v0,当杆对球的作用力为零时,
mg=m$\frac{{{v}_{0}}^{2}}{L}$得v0=$\sqrt{gL}$=2m/s
(1)当v1=1m/s<v0时,A受杆的支持力FN1,有mg-FN1=m$\frac{{{v}_{1}}^{2}}{L}$得:FN1=15N
(2)、当v2=4m/s>v0时,A受杆向下的拉力FN2,有mg+FN2=m$\frac{{{v}_{2}}^{2}}{L}$得:FN2=60N
由牛顿第三定律得:当v1=1m/s时,杆受到的力大小为为15N,方向向下;当v1=4m/s 时,杆受到的力大小为为60N,方向向上
答:(1)当v1=1m/s时,杆受到的力大小为为15N,方向向下;
(2)当v1=4m/s 时,杆受到的力大小为为60N,方向向上.
点评 解决本题的关键知道小球做圆周运动向心力的来源,结合牛顿第二定律进行求解,难度不大.

练习册系列答案
相关题目
11.历史上有些科学家曾把在相等位移内速度变化相等的单向直线运动称为“匀变速直线运动”(现称“另类匀变速直线运动”),“另类加速度”定义为A=$\frac{{{V_t}-{V_0}}}{S}$,其中V0和Vt分别表示某段位移S内的初速度和末速度.A>0表示物体做加速运动,A<0表示物体做减速运动.而现在物理学中加速度定义式为a=$\frac{{{V_t}-{V_0}}}{t}$,下列说法正确的是( )
| A. | 若A不变,则a也不变 | |
| B. | 若A>0且保持不变,则a逐渐变大 | |
| C. | 若A>0且保持不变,则a逐渐变小 | |
| D. | 若A不变,则物体在中间位置处的速度为$\sqrt{\frac{{v}_{t}^{2}+{v}_{0}^{2}}{2}}$ |
8. 匀强电场中的三点A、B、C是三角形的三个顶点,AB的长度为1m,D为AB的中点,如图所示.已知电场线平行于△ABC所在平面,A、B、C三点的电势分别为14V、6V和2V.设场强大小为E,一电荷量为1×10-6C的正电荷从D点移到C点电场力所做的功为W,则( )
匀强电场中的三点A、B、C是三角形的三个顶点,AB的长度为1m,D为AB的中点,如图所示.已知电场线平行于△ABC所在平面,A、B、C三点的电势分别为14V、6V和2V.设场强大小为E,一电荷量为1×10-6C的正电荷从D点移到C点电场力所做的功为W,则( )
 匀强电场中的三点A、B、C是三角形的三个顶点,AB的长度为1m,D为AB的中点,如图所示.已知电场线平行于△ABC所在平面,A、B、C三点的电势分别为14V、6V和2V.设场强大小为E,一电荷量为1×10-6C的正电荷从D点移到C点电场力所做的功为W,则( )
匀强电场中的三点A、B、C是三角形的三个顶点,AB的长度为1m,D为AB的中点,如图所示.已知电场线平行于△ABC所在平面,A、B、C三点的电势分别为14V、6V和2V.设场强大小为E,一电荷量为1×10-6C的正电荷从D点移到C点电场力所做的功为W,则( )| A. | W=8×10-6J,E≤6V/m | B. | W=6×10-6J,E>6V/m | ||
| C. | W=6×10-6J,E≤8V/m | D. | W=8×10-6J,E>8V/m |
15.以下说法正确的是( )
| A. | 机械波与电磁波均要通过介质才能传播 | |
| B. | 机械波和电磁波在介质中的传播速度均与介质有关、与波的频率无关 | |
| C. | 物体做受迫振动的频率由驱动力的频率决定,与固有频率无关 | |
| D. | LC振荡的周期不仅跟电感与电容有关,而且还与电路中的振荡能量多少有关 |
5.一物体做阻尼振动,下列说法正确的是( )
| A. | 振幅随时间减小 | B. | 周期保持不变 | ||
| C. | 机械能随时间减小 | D. | 周期随时间减小 |
 如图,变压器的原线圈接到220V的交流电源上,副线圈有两个,副线圈2 的匝数n2=30匝,与一个标有“12V 12W”的灯泡组成闭合回路,且灯泡L正常发光,副线圈3的输出电压U3=110V,与电阻R组成闭合回路,通过电阻R的电流强度为0.4A,求
如图,变压器的原线圈接到220V的交流电源上,副线圈有两个,副线圈2 的匝数n2=30匝,与一个标有“12V 12W”的灯泡组成闭合回路,且灯泡L正常发光,副线圈3的输出电压U3=110V,与电阻R组成闭合回路,通过电阻R的电流强度为0.4A,求