题目内容
6.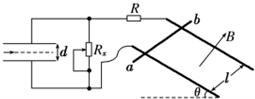 如图所示,质量为M=2kg的导体棒ab,垂直放在相距为l=1m的平行光滑金属轨道上.导轨平面与水平面的夹角为θ=30°,并处于磁感应强度大小为B=2T、方向垂直与导轨平面向上的匀强磁场中,左侧是水平放置,间距为d=0.5m的平行金属板,R和Rx分别表示定值和滑动变阻器的阻值,定值电阻为R=3Ω,不计其他电阻.现将金属棒由静止释放,重力加速度为g=10m/s2,试求:
如图所示,质量为M=2kg的导体棒ab,垂直放在相距为l=1m的平行光滑金属轨道上.导轨平面与水平面的夹角为θ=30°,并处于磁感应强度大小为B=2T、方向垂直与导轨平面向上的匀强磁场中,左侧是水平放置,间距为d=0.5m的平行金属板,R和Rx分别表示定值和滑动变阻器的阻值,定值电阻为R=3Ω,不计其他电阻.现将金属棒由静止释放,重力加速度为g=10m/s2,试求:(1)调节Rx=R,释放导体棒,当棒沿导轨匀速下滑时,求通过棒的电流I及棒的速率v;
(2)改变Rx,待棒沿导轨再次匀速下滑后,将质量为m=3×10-4kg、带电量为+q=5×10-5C的微粒水平射入金属板间,若它恰能匀速通过,求此时的Rx.
分析 (1)ab棒匀速下滑时,受力平衡,由平衡条件求电流I.由电磁感应定律求电动势E=BLv、闭合电路欧姆定律求速度v.
(2)由带电粒子的匀速通过电容器求电压,结合欧姆定律求出滑动变阻器阻值.
解答 解:(1)ab匀速下滑处于平衡状态,由平衡条件得:Mgsinθ=BIl,
解得,通过棒的电流为:I=$\frac{Mgsinθ}{Bl}$=$\frac{2×10sin30°}{2×1}$=5A;
感应电流:I=$\frac{Blv}{R+{R}_{x}}$,解得:v=$\frac{I(R+{R}_{X})}{Bl}$=$\frac{5×(3+3)}{2×1}$=15m/s;
(2)微粒在板间做匀速直线运动,
由平衡条件得:q$\frac{U}{d}$=mg,
由欧姆定律得:Rx=$\frac{U}{I}$,
解得:Rx=$\frac{mBdl}{Mqsinθ}$=$\frac{3×1{0}^{-4}×2×0.5×1}{2×5×1{0}^{-5}sin30°}$=12Ω;
答:(1)通过棒的电流I为5A,棒的速率v为15m/s;
(2)此时的Rx为12Ω.
点评 本题是导体在导轨上滑动和磁流体发电机的综合类型,从力和能量两个角度研究,关键要掌握法拉第定律、欧姆定律等等基本规律,并能正确运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.2016年2月11日,美国科学家宣布探测到引力波,证实了爱因斯坦100年前的预测,弥补了爱因斯坦广义相对论中最后一块缺失的“拼图”.双星的运动是产生引力波的来源之一,假设宇宙中有一双星系统由a、b两颗星体组成,这两颗星绕它们连线的某一点在万有引力作用下作匀速圆周运动,测得a星的周期为T,a、b两颗星的距离为l、a、b两颗星的轨道半径之差为△r(a星的轨道半径大于b星的),则( )
| A. | b星公转的周期为$\frac{l-△r}{l+△r}$T | B. | a、b两颗星的半径之比为$\frac{l}{l-△r}$ | ||
| C. | a星公转的线速度大小为$\frac{π(l+△r)}{T}$ | D. | a、b两颗星的质量之比为$\frac{l-△r}{l+△r}$ |
15.保持入射光线方向不变,将平面镜绕着过入射点且垂直于入射光线和法线所决定的平面的轴旋转θ角,则( )
| A. | 反射光线也转过θ角 | |
| B. | 反射光线转过2θ角 | |
| C. | 入射角增大2θ角 | |
| D. | 反射光线与入射光线的夹角增大θ角 |
16.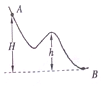 某游客领着孩子爬山时,不小心将手中的皮球滑落,皮球从A点滚到了山脚下的B点,高度标记如图所示,皮球从A运动到B点的过程中( )
某游客领着孩子爬山时,不小心将手中的皮球滑落,皮球从A点滚到了山脚下的B点,高度标记如图所示,皮球从A运动到B点的过程中( )
 某游客领着孩子爬山时,不小心将手中的皮球滑落,皮球从A点滚到了山脚下的B点,高度标记如图所示,皮球从A运动到B点的过程中( )
某游客领着孩子爬山时,不小心将手中的皮球滑落,皮球从A点滚到了山脚下的B点,高度标记如图所示,皮球从A运动到B点的过程中( )| A. | 运动轨迹未知,无法求出重力做的功 | |
| B. | 阻力大小未知,无法求出重力做的功 | |
| C. | 重力做功mg(H-h) | |
| D. | 重力做功mgH |
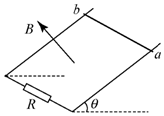 如图所示,两平行金属导轨电阻不计,相距L=1m,导轨平面与水平面的夹角θ=37°,导轨的下端连接一个电阻R.匀强磁场的方向垂直于导轨平面向上,磁感应强度为B=0.4T.质量为0.2kg、电阻不计的金属棒垂直放在两导轨上且保持良好接触,金属棒和导轨间的动摩擦因数为μ=0.25.金属棒沿导轨由静止开始下滑,当金属棒下滑的速度达到稳定时,其速度的大小为10m/s.g取10m/s2,已知sin37°=0.6,cos37°=0.8,求:
如图所示,两平行金属导轨电阻不计,相距L=1m,导轨平面与水平面的夹角θ=37°,导轨的下端连接一个电阻R.匀强磁场的方向垂直于导轨平面向上,磁感应强度为B=0.4T.质量为0.2kg、电阻不计的金属棒垂直放在两导轨上且保持良好接触,金属棒和导轨间的动摩擦因数为μ=0.25.金属棒沿导轨由静止开始下滑,当金属棒下滑的速度达到稳定时,其速度的大小为10m/s.g取10m/s2,已知sin37°=0.6,cos37°=0.8,求:
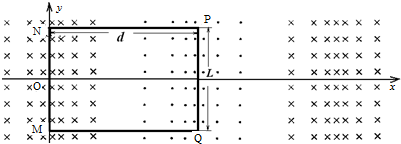
 如图所示,MN、PQ为相距L的光滑平行的金属导轨,导轨平面与水平面夹角为θ,导轨处于磁感应强度为B、方向垂直于导轨平面向上的匀强磁场中,在两导轨间接有一电阻为R的定值电阻,质量为m的导体棒从ab处由静止开始下滑,加速运动到位置cd处时棒的速度大小为v,此过程中通过电阻的电量为q,除R外,回路其余电阻不计,求:
如图所示,MN、PQ为相距L的光滑平行的金属导轨,导轨平面与水平面夹角为θ,导轨处于磁感应强度为B、方向垂直于导轨平面向上的匀强磁场中,在两导轨间接有一电阻为R的定值电阻,质量为m的导体棒从ab处由静止开始下滑,加速运动到位置cd处时棒的速度大小为v,此过程中通过电阻的电量为q,除R外,回路其余电阻不计,求: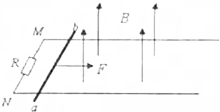 两根足够长且平行的光滑金属导轨M、N水平固定放置,电阻忽略不计,两导轨左端连接有一阻值为R的电阻,导轨间存在竖直向上的匀强磁场,将一质量为m的导体棒ab放置在两导轨上,并始终保持与导轨垂直接触,导体棒接入导轨间部分的电阻值为r,现出现与导体棒施加一大小恒为F的水平向右拉力,使之从静止开始运动,如图所示,在导体棒ab运动了x的距离时,测得其速度为v,重力加速度为g,试求:
两根足够长且平行的光滑金属导轨M、N水平固定放置,电阻忽略不计,两导轨左端连接有一阻值为R的电阻,导轨间存在竖直向上的匀强磁场,将一质量为m的导体棒ab放置在两导轨上,并始终保持与导轨垂直接触,导体棒接入导轨间部分的电阻值为r,现出现与导体棒施加一大小恒为F的水平向右拉力,使之从静止开始运动,如图所示,在导体棒ab运动了x的距离时,测得其速度为v,重力加速度为g,试求: