题目内容
12. 质量为m,电荷量为q的粒子,以初速度v垂直进入磁感应强度为B,宽度为L的匀强磁场区域,并从另一端出射,如图所示,不计粒子重力.求
质量为m,电荷量为q的粒子,以初速度v垂直进入磁感应强度为B,宽度为L的匀强磁场区域,并从另一端出射,如图所示,不计粒子重力.求(1)带电粒子运动的轨道半径R;
(2)带电粒子离开磁场时的偏转角的θ;
(3)带电粒子在磁场中的运动时间t.
分析 (1)根据洛伦兹力充当向心力列式可求得轨道半径;
(2)根据几何关系可求出半径与磁场宽度之间的关系,则可求出对应的偏向角;
(3)根据v=$\frac{2πr}{T}$可求得周期,再根据几何关系求出圆心角;则由t=$\frac{θ}{2π}T$可求出对应的时间.
解答  解:(1)洛伦兹力充当向心力,故有:$qBv=m\frac{v^2}{R}$,
解:(1)洛伦兹力充当向心力,故有:$qBv=m\frac{v^2}{R}$,
解得:$R=\frac{mv}{Bq}$
(2)粒子运动轨迹如图所示,根据几何知识可得:
$R=\frac{L}{sinθ}$,
故有:$θ=arcsin\frac{L}{R}=arcsin\frac{qBL}{mv}$
(3)根据公式$T=\frac{2πr}{v}$
可得:$T=\frac{2πm}{Bq}$,
故有:$t=\frac{θm}{Bq}=\frac{m}{Bq}arcsin\frac{qBL}{{m{v_0}}}$
答:(1)带电粒子运动的轨道半径R为$\frac{mv}{Bq}$
(2)带电粒子离开磁场时的偏转角的θ为arcsin$\frac{qEL}{mv}$
(3)带电粒子在磁场中的运动时间t为$\frac{m}{Bq}arcsin\frac{qBL}{m{v}_{0}}$.
点评 本题考查带电粒子在磁场中的运动问题,要注意明确此类问题的关键在于“定圆心、求半径”;本题中是根据洛伦兹力充当向心力求出半径,再利用几何关系求解偏转角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18. 地球是一个大磁体:
地球是一个大磁体:
①在地面上放置一个小磁体,小磁体的南极指向地磁场的南极;
②地磁场的北极在地理南极附近;
③赤道附近磁场的方向和地面平行;
④北半球地磁场方向相对地面是斜向上的;
⑤地球上任何地方的地磁场方向都是和地面平行的.
以上关于地磁场的描述正确的是( )
 地球是一个大磁体:
地球是一个大磁体:①在地面上放置一个小磁体,小磁体的南极指向地磁场的南极;
②地磁场的北极在地理南极附近;
③赤道附近磁场的方向和地面平行;
④北半球地磁场方向相对地面是斜向上的;
⑤地球上任何地方的地磁场方向都是和地面平行的.
以上关于地磁场的描述正确的是( )
| A. | ①②④ | B. | ②③④ | C. | ②③ | D. | ①⑤ |
19.下列各组物理量中,都是矢量的是( )
| A. | 质量、位移、速度 | B. | 速度、速率、加速度 | ||
| C. | 速度的变化、时间、位移 | D. | 力、加速度、速度 |
16. 如图所示,一个光滑的半径为R的内凹圆槽固定在竖直平面内,O为圆槽的圆心.两金属小球用轻杆连接,置于圆槽内.甲球质量为2m,初位置与O点在同一水平直线上,乙球质量为m,初位置在O点正下方.如果由初位置释放甲、乙两球,则下列说法不正确的是( )
如图所示,一个光滑的半径为R的内凹圆槽固定在竖直平面内,O为圆槽的圆心.两金属小球用轻杆连接,置于圆槽内.甲球质量为2m,初位置与O点在同一水平直线上,乙球质量为m,初位置在O点正下方.如果由初位置释放甲、乙两球,则下列说法不正确的是( )
 如图所示,一个光滑的半径为R的内凹圆槽固定在竖直平面内,O为圆槽的圆心.两金属小球用轻杆连接,置于圆槽内.甲球质量为2m,初位置与O点在同一水平直线上,乙球质量为m,初位置在O点正下方.如果由初位置释放甲、乙两球,则下列说法不正确的是( )
如图所示,一个光滑的半径为R的内凹圆槽固定在竖直平面内,O为圆槽的圆心.两金属小球用轻杆连接,置于圆槽内.甲球质量为2m,初位置与O点在同一水平直线上,乙球质量为m,初位置在O点正下方.如果由初位置释放甲、乙两球,则下列说法不正确的是( )| A. | 甲球可沿凹槽下滑到槽的最低点 | |
| B. | 下滑过程中甲球减少的机械能总等于乙球增加的机械能 | |
| C. | 下滑过程中甲球减少的重力势能总等于乙球增加的机械能 | |
| D. | 杆从右向左滑回时,乙球一定能回到凹槽的最低点 |
4.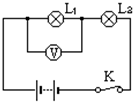 如图所示电路,电源电压为10V,闭合电键K后,电压表读数约为10V,L1发光,L2不发光,可能的情况是( )
如图所示电路,电源电压为10V,闭合电键K后,电压表读数约为10V,L1发光,L2不发光,可能的情况是( )
 如图所示电路,电源电压为10V,闭合电键K后,电压表读数约为10V,L1发光,L2不发光,可能的情况是( )
如图所示电路,电源电压为10V,闭合电键K后,电压表读数约为10V,L1发光,L2不发光,可能的情况是( )| A. | L1处短路 | B. | L2处短路 | C. | L1灯丝断了 | D. | L2灯丝断了 |
 质量为m的物体在与水平方向成α角的斜向上的拉力F的作用下,沿水平面匀速运动,如图所示.求物体与接触面间的动摩擦因数.
质量为m的物体在与水平方向成α角的斜向上的拉力F的作用下,沿水平面匀速运动,如图所示.求物体与接触面间的动摩擦因数. 质量为10kg的物体在F=200N的水平推力作用下,从固定斜面底端由静止开始沿斜面向上运动,已知斜面的倾角θ=37°,物体与斜面间的动摩擦因数μ=0.2,斜面足够长.求(已知sin37°=0.6,cos37°=0.8,重力加速度g取10m/s2)
质量为10kg的物体在F=200N的水平推力作用下,从固定斜面底端由静止开始沿斜面向上运动,已知斜面的倾角θ=37°,物体与斜面间的动摩擦因数μ=0.2,斜面足够长.求(已知sin37°=0.6,cos37°=0.8,重力加速度g取10m/s2)