题目内容
19. 如图所示,一带电微粒质量m=2.0×10-11kg、电荷量q=1.0×10-5C,从静止开始经电压为U1=100V的电场加速后,水平进入两平行金属板间的偏转电场,微粒射出偏转电场时的偏转角θ=60°,已知偏转电场金属板长L=2$\sqrt{3}$cm,重力忽略不计,求:
如图所示,一带电微粒质量m=2.0×10-11kg、电荷量q=1.0×10-5C,从静止开始经电压为U1=100V的电场加速后,水平进入两平行金属板间的偏转电场,微粒射出偏转电场时的偏转角θ=60°,已知偏转电场金属板长L=2$\sqrt{3}$cm,重力忽略不计,求:(1)带电微粒经U1=100V的电场加速后的速率;
(2)两金属板间偏转电场的电场强度E的大小.
分析 (1)根据动能定理求出带电粒子经U1=100V的电场加速后的速率;
(2)带电粒子在偏转电场中做类平抛运动,将该运动分解,在水平方向上做匀速直线运动,在竖直方向上做初速度为零的匀加速直线运动,抓住等时性,结合运动学公式和牛顿第二定理求出偏转电场的电场强度.
解答 解:(1)设带电微粒经加速电场加速后的速率为v1.
根据动能定理:$q{U}_{1}=\frac{1}{2}m{{v}_{1}}^{2}$,
解得:${v}_{1}=\sqrt{\frac{2q{U}_{1}}{m}}$=$\sqrt{\frac{2×1{0}^{-5}×100}{2×1{0}^{-11}}}m/s=1{0}^{4}m/s$.
(2)带电微粒在偏转电场中只受电场力作用,做类平抛运动.
水平方向:L=v1t,
竖直方向:a=$\frac{qE}{m}$,
v2=at,
又$tanθ=\frac{{v}_{2}}{{v}_{1}}$,
代入数据解得:E=104V/m.
答:(1)带电微粒经U1=100V的电场加速后的速率为104m/s;
(2)两金属板间偏转电场的电场强度E的大小为104V/m.
点评 本题考查了带电粒子的加速和偏转,关键掌握处理类平抛运动的方法,结合牛顿第二定律和运动学公式综合求解,难度不大.

练习册系列答案
相关题目
10.某质点的v-t图象如图所示,则( )


| A. | 前2s质点做匀加速直线运动 | B. | 4~6 s内质点匀速直线运动 | ||
| C. | 3 s末质点速度是5 m/s | D. | 8 s末质点回到原出发点 |
7.完全相同的两金属小球,相距为d(d远大于小球的直径),分别带有q和3q的电荷量,其相互作用的引力为F,现将两小球接触,然后分开,放回原处,则它们相互作用的库伦力为( )
| A. | $\frac{F}{3}$,引力 | B. | $\frac{F}{3}$,斥力 | C. | $\frac{4F}{3}$,引力 | D. | $\frac{4F}{3}$,斥力 |
4.金属小球A带+3Q的电荷量,另一个完全相同的金属小球B带-Q的电荷量,将两小球接触后再分开,则B球的电荷量为( )
| A. | 0 | B. | +Q | C. | +2Q | D. | +3Q |
11.下列说法正确的是( )
| A. | 给电风扇供电时,电能全部转化为机械能 | |
| B. | 给电风扇供电时,电能主要转化为内能 | |
| C. | 给电热器供电时,电能几乎全部转化为内能 | |
| D. | 给电热器供电时,只有很少一部分电能转化为内能 |
20.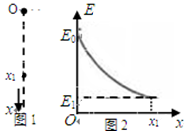 某空间区域的竖直平面内存在电场,其中竖直的一条电场线如图1中虚线所示.一个质量为m、电荷量为q的带正电小球,在电场中从O点由静止开始沿电场线竖直向下运动.以O为坐标原点,取竖直向下为x轴的正方向,小球的机械能E与位移x的关系如图2所示,不计空气阻力.则( )
某空间区域的竖直平面内存在电场,其中竖直的一条电场线如图1中虚线所示.一个质量为m、电荷量为q的带正电小球,在电场中从O点由静止开始沿电场线竖直向下运动.以O为坐标原点,取竖直向下为x轴的正方向,小球的机械能E与位移x的关系如图2所示,不计空气阻力.则( )
 某空间区域的竖直平面内存在电场,其中竖直的一条电场线如图1中虚线所示.一个质量为m、电荷量为q的带正电小球,在电场中从O点由静止开始沿电场线竖直向下运动.以O为坐标原点,取竖直向下为x轴的正方向,小球的机械能E与位移x的关系如图2所示,不计空气阻力.则( )
某空间区域的竖直平面内存在电场,其中竖直的一条电场线如图1中虚线所示.一个质量为m、电荷量为q的带正电小球,在电场中从O点由静止开始沿电场线竖直向下运动.以O为坐标原点,取竖直向下为x轴的正方向,小球的机械能E与位移x的关系如图2所示,不计空气阻力.则( )| A. | 从O到x1的过程中,小球的速率越来越大,加速度越来越大 | |
| B. | 电场强度大小恒定,方向沿x轴负方向 | |
| C. | 从O到x1的过程中,相等的位移内,小球克服电场力做的功相等 | |
| D. | 到达x1位置时,小球速度的大小为$\sqrt{\frac{2({E}_{1}-{E}_{0}+mg{x}_{1})}{m}}$ |

 用螺旋测微器测量一根合金丝的直径,为防止读数时测微螺杆发生转动,读数前应先旋紧图示的部件C(选填“A”、“B”、“C”或“D”),从图中的示数可读出合金丝的直径为0.410mm.
用螺旋测微器测量一根合金丝的直径,为防止读数时测微螺杆发生转动,读数前应先旋紧图示的部件C(选填“A”、“B”、“C”或“D”),从图中的示数可读出合金丝的直径为0.410mm.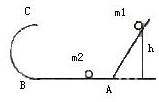 如图所示半圆轨道直径BC=0.8m,水平轨道上AB=1.6m.m1,m2均为0.1kg的弹性球.若m1由高h处开始下滑与静止在A处的球m2发生正碰,碰后m2运动经C点抛出后又与m1相碰,求:
如图所示半圆轨道直径BC=0.8m,水平轨道上AB=1.6m.m1,m2均为0.1kg的弹性球.若m1由高h处开始下滑与静止在A处的球m2发生正碰,碰后m2运动经C点抛出后又与m1相碰,求: